Logarithm is the reverse operation of exponentiation.
Logarithms were first introduced in astronomy to simplify the calculation of large numbers, and are used to determine the pH of solutions, the scale for the volume of sound, and the scale for determining the brightness of stars.
Let's look at the following example of how to introduce a logarithm:
In the above example, the number y was not difficult to find. In general, however, such an exponent (number y) is found only by means of a logarithm.
The logarithm of a positive real number x with respect to base a is the exponent y by which a must be raised to yield x.
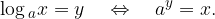
Let's look at the elements of the logarithm:
Let's look at a few more examples:
The decimal logarithm is the logarithm with base 10.
By agreement, we do not write the base for the decimal logarithm of:
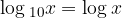
When calculating the decimal logarithm, we can use a pocket calculator that contains the appropriate key log.
The natural logarithm is the logarithm with the base e.
The following designation has been applied to the natural logarithm:
When calculating the natural logarithm, we can use a pocket calculator that contains the appropriate key ln.
The concept of logarithm is used to change an exponential equation:
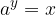
into a logarithmic equation:
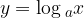
antilogarithm, on the other hand, translates the logarithmic equation into an exponential equation. Logarithm and anti-logarithm are therefore reverse operations.
If the logarithmic and exponential functions occur together, one as an exponent, the other as a base, or vice versa, for each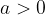 
the following holds:
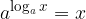
and
The logarithm of the product of numbers greater than 0 is equal to the sum of the logarithms of the individual factors:
The logarithm of the product is the sum of the logarithms:
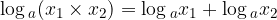
Let us prove the above equality. Let them be
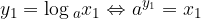
and
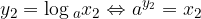
Let's write down the product:
If we logarithmize the above expression we get:
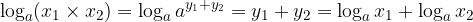
The logarithm of the quotient of numbers greater than 0 is equal to the difference between the logarithms of the divisor and the divisor.
The logarithm of the quotient is equal to the difference of the logarithms:
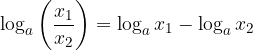
The proof is similar to the previous one.
The logarithm of the power is equal to the product of the exponent and the logarithm of the base.
Logarithm of power:
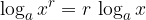
Let's prove it. Let it be
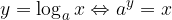
Then follows:
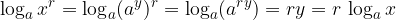
When calculating cases in which logarithms occur, we often want to use a computer that calculates only the decimal and natural logarithms. Therefore, we convert the logarithm to the appropriate base:
When moving from the base b to the new base a we use the form:
Let's run the form. The logarithm with base b is denoted by
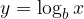
which by definition is written as
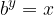
The above equality is logarithmized with a logarithm based on a and the power logarithm is used.
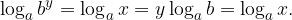
Now y replace with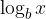 
and get the connection:
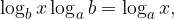
which, after transformation, is the same as our form:
