The strength of a magnetic field (or magnetic field strength) is best understood if we draw a comparison between electric and magnetic fields. To compare with magnetic field strength, let's look back at electric field strength.
In the material, Electric field strength, we saw that an electric charge creates an electric field in its surroundings. At each point of the field, we can determine the electric field strength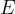 
. We also wrote down the law of electric flux which says:
if the surface area 
encloses all lines of the electric field caused by the charge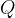 
, then,
the electric flux through this surface is equal to the charge itself.
We expressed it mathematically as:
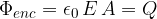
With the help of this law, we calculated the electric field strength 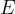around simple electrically charged bodies.
We want to evaluate the magnetic field in a similar way. For this purpose, we introduce the magnetic field strength which is denoted by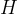 
. The condition for the formation of a magnetic field with an electric charge is that the electric charge moves. A moving charge is an electric current.
Electric current and magnetic field strength are related via Ampere's law of magnetic voltage.
Magnetic field strength is not part of the high school physics curriculum. In the explanation, we will start from the equation of Ampere's law, which describes the magnetic voltage. The derivation of this equation is discussed at the university level, we just write it down here.
This law takes into account the possibility of having several parallel conductors next to each other through which the current flows in the same direction. All currents therefore contribute to the total magnetic field. Ampere's law of magnetic voltage is given in simplified form as:
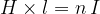
where:
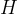- magnetic field strength,
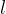- length of the line enclosing the conductor,
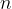- number of parallel conductors,
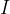- electric current through conductors.
The term 
is also called magnetic voltage, so this law is called Ampere’s law of magnetic voltage.
From the above equation, we obtain the magnetic field strength 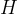which will therefore be given as:
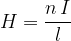
The unit is 
.
With the help of Ampere's law, we can calculate the magnetic field strength around a straight conductor or a long and narrow coil.
The magnetic field strength is proportional to the current and inversely proportional to the length of the line surrounding one or more current conductors.
Among other things, the strength of the magnetic field makes it easier for us to calculate its density.
Let's take a wire through which an electric current flows, as shown in the figure below.
The magnetic field around a straight current-carrying conductor has the form of concentric circles. This can be determined with the help of iron filings or with a magnetic needle - a magnet, which will always be placed tangentially to the magnetic field line.
We choose a point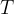 
in the space around the current-carrying conductor and calculate the magnetic field strength :
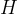The direction of the vector 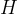is obtained using the right-hand rule: the thumb of the right hand is aligned with the direction of the current in the wire, and the fingers wrapped around the conductor indicate the direction of the magnetic field forces. The vector 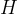has a direction tangent to the force line at that point.
The lines of force in a straight wire are closed curves without a beginning and without an end. The magnetic field therefore does not have clearly defined poles, like an electric charge. We cannot determine the north and south poles of the "magnet".
A coil is a wire wound on a narrow cylinder. Each turn of wire is a current loop that creates a magnetic field. If a coil has 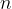turns, the strength of the magnetic field inside the coil is 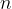times the magnetic field caused by a single current loop.
The magnetic field of the individual turns is added together inside the coil. If the coil is long and narrow, we can consider the field inside the coil to be homogeneous. A magnetic field is homogeneous if the lines of the magnetic field are equally dense, straight, and parallel everywhere. In this case, the magnetic field strength inside the coil is independent of the point of observation.
The direction of the magnetic field of the coil can be determined by:
magnet,
using the right-hand rule, or
right screw.
A coil is drawn on the left in the figure above. Let's observe the current through the threads. To determine the direction of the field, it is enough to observe the current through a single thread, since the current flows through all the threads in the same direction. According to the right-hand rule, the current inside the coil causes a magnetic field that runs from the lower part of the coil to the upper part. The force lines emerge from the top of the coil. Similar to a bar magnet, we consider this to be the north pole (N) of the coil. Below the coil, the force lines enter the coil, so this is the south pole (S).
The coil can also be drawn in cross-section - the figure on the right above. The image helps us to determine the direction of the magnetic field, as it makes it easier for us to imagine the direction of the current. On the left side of the coil are the cross-sections of the threads, where the current flows from the screen towards us (circle with a dot). On the right side of the coil, in the screen (circle with a cross).
Inside the coil, the lines are equally dense and parallel. This is also where the strongest field is. The field is homogeneous. Outside the coil, the lines expand and the magnetic field strength drops to practically zero. The forces are always closed curves. They have no beginning and no end, unlike electric lines, which arise from a positive charge and sink into a negative charge.
For an approximate calculation of the magnetic field strength in the coil, we can use Ampere's law, where we assume that the length of the wire is exactly the same as the length of the coil.
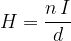
where 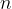is the number of turns of the coil.
