Electrons, each of mass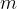 
and charge 
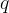, are accelerated from rest in a vacuum through a potential difference 
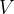. Derive an expression, in terms of 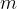, 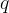and 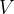, for the final speed 
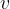of the electrons. Explain your working.
The accelerated electrons in (a) are injected at point S into a region of uniform magnetic field of flux density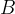 
, as illustrated in the figure below.
The electrons move at right angles to the direction of the magnetic field. The path of the electrons is a circle of radius 
.
Show that the specific charge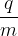 
of the electrons is given by the expression
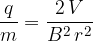
Explain your working.
Electrons are accelerated through a potential difference 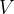of 
. The electrons are injected normally into the magnetic field of flux density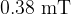 
. The radius of the circular orbit of the electrons is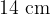 
. Use this information to calculate a value for the specific charge of an electron.
Suggest why the arrangement outlined in (ii), using the same values of 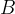and 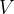, is not practical for the determination of the specific charge of 
-particles.
is equal to the change in kinetic energy 
of the electron:
.
