Personal collections


The magnetic flux  is equal to the product of the magnetic field density
is equal to the product of the magnetic field density 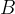 and the surface area through which the magnetic field lines pass and which is perpendicular to the lines. If the area
and the surface area through which the magnetic field lines pass and which is perpendicular to the lines. If the area  is not perpendicular to the lines of force, we take the component of the area that is perpendicular to the lines of force of the magnetic field.
is not perpendicular to the lines of force, we take the component of the area that is perpendicular to the lines of force of the magnetic field.

The magnetic flux unit is:

Let's imagine that a wire loop encloses the surface area  . If the magnetic flux
. If the magnetic flux  through the loop changes with time
through the loop changes with time 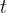 , a voltage is induced in it. The voltage
, a voltage is induced in it. The voltage 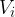 induced is given as:
induced is given as:
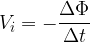
If there are 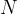 turns of the loop, the induced voltage is:
turns of the loop, the induced voltage is:

The magnetic flux through the loop changes if the surface 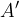 or the magnetic field density
or the magnetic field density 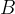 changes with time - see equation (1). Therefore:
changes with time - see equation (1). Therefore:

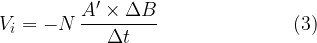
Let's assume we have a coil with 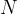 turns and a cross-sectional area
turns and a cross-sectional area  . The current
. The current 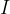 through the coil changes over time
through the coil changes over time 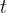 . Due to the change in current, the magnetic flux through the coil also changes. The result is an induced voltage
. Due to the change in current, the magnetic flux through the coil also changes. The result is an induced voltage 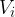 , which is calculated using equation (3) above:
, which is calculated using equation (3) above:
The first factor in the right-hand side of the above equation depends only on the coil itself (number of turns, area, and the substance of the coil). We call it inductance. Let us denote it by L:
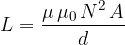
The unit for inductance is 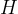 (Henry):
(Henry):
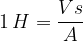
The induced voltage can now be written in the form:

Why did we put a minus sign in the equation for induced voltage?
This is according to Lenz's rule which states that the direction of the induced voltage is such that the current it drives inhibits the cause of the induced voltage (change in magnetic flux).