

Mathematical induction is a method by which we check the validity of an assumption for all natural numbers. As a proof tool, it is useful in many areas of mathematics.
We use mathematical induction to prove the validity of a formula, a statement, an equation, a property etc in a set of natural numbers. Proof by mathematical induction is based on two steps:
first, we prove the mathematical statement for the first natural number, the number 1. It is quite expected that if the statement holds for the whole set of natural numbers 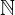 , then it certainly holds for the natural number 1. If the statement does not hold, then the statement is false. However, if the claim is valid, we proceed to the second step.
, then it certainly holds for the natural number 1. If the statement does not hold, then the statement is false. However, if the claim is valid, we proceed to the second step.
secondly, we want to prove that the given mathematical statement is valid, in addition to the natural number 1, for all other cases. We do this by:
first assuming that the statement holds for a natural number n
then, assuming that n holds, we prove that it also holds for n + 1
If, assuming that the statement holds for a natural number n, we prove that it also holds for n + 1, we have proved the mathematical statement - by means of mathematical induction. They proved it because:
should be our n = 1. If the statement holds for n = 1, then it holds (proved in the second step of proving by induction) also for n + 1 = 2. However, since in the first step of proving by induction we have shown that the statement for n = 1 holds, it follows that the statement also holds for n = 2.
since we have just found that the statement holds for n = 2, it follows from the second induction step that if the statement holds for n = 2, it also holds for n + 1 = 3
and if the statement holds for n = 3, it also holds for n + 1 = 4, and such a conclusion can be repeated indefinitely, for any natural number.
Mathematical induction:
in the first step, we check whether the given mathematical statement is valid for the first natural number, that is if it is valid for 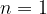 ;
;
in the second step:
We set the induction assumption:
"if the statement holds for some natural number 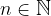 , then it also holds for its successor
, then it also holds for its successor 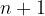 "
"
and the induction assumption is proved.
With the validity of both steps, the claim is proved for all natural numbers.
Sometimes a particular statement does not apply to all natural numbers, but only to all natural numbers within a certain interval. Such an example is e.g. diagonals in a regular n-gon:
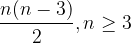
To solve such problems, we change the proof procedure by not proving the statement for the first natural number, but for the first number when our statement is valid (i.e., for 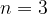 ). The second step remains unchanged.
). The second step remains unchanged.
We have the sequence 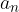 . We want to calculate the sum of the first n terms of the sequence but we are not sure if the given form
. We want to calculate the sum of the first n terms of the sequence but we are not sure if the given form  is correct. With the help of mathematical induction, the correctness and generality of the formula
is correct. With the help of mathematical induction, the correctness and generality of the formula  can be checked in two steps:
can be checked in two steps:
check if: 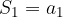
then check if: 
By validating both steps, we prove that the formula  is valid for each
is valid for each 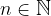 .
.