Personal collections


In general, measurement means the definition of properties of objects or people with numerical values. The measured quantity is compared with the basic unit of measurement, which is determined by an international standard.
In geometry, measurement is the basis for sizing geometric elements, figures, and bodies.
The measurement can refer to one (length, width, height, depth), two (area, surface) or three (volume) spatial dimensions, and a special category is the angle used to define the size of a plane sandwiched between two lines.
Length is a physical quantity, which means the distance between two points. It is generally denoted by the lowercase letter l, and in plane geometry, it is denoted in the same way as the line to which it refers (e.g. the sides of figures with a, b, c, d, diagonals with e, f and so on)
In addition to the expression 'length', we also use the terms width, height and depth for distances.
The basic unit of measurement for length is metre. Let us mark it with a small letter m.
In addition to the basic, we also know larger and smaller units of length. The most commonly used are shown in the following table:
The blue text in the table above represents the destinal prefix. Each prefix represents a certain power of 10 with an integer exponent, by which we must multiply the base unit to obtain a unit with this prefix.
The following table can be used to convert between units of length:
In the first row of the table write the length in the given unit of measure, and from the second row read the same length in the searched unit of measure.
Let's look at the use of the table in the following examples:
Area is a measure of the size of geometric figures.
The basic unit of measurement for area is the square metre, labeled with 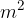 .
.
In addition to the basic unit, we also know larger and smaller units of measurement for the area or surface. The most commonly used are shown in the following table:
The blue text in the table above represents the destinal prefix. Each prefix represents a certain power of 10 with an integer exponent, by which we must multiply the base unit to obtain a unit with this prefix. Since in the case of area we use the square of the basic unit of measurement for length on the surface, the prefix is also squared.
The following table can be used to convert between units of measure for an area:
In the first row of the table we write the area in the given unit of measure, and from the second row we read the same area in the searched unit of measure.
Let's look at the use of the table in the following examples:
We usually do not measure the plane, but calculate it on the basis of measuring length and using mathematical equations.
The actual measurement of the area can be performed, among other things, by dividing into unit squares (with a side length equal to one unit) and counting these squares, but the method is not accurate, and its interpretation goes beyond the content of the textbook.
Volume is a measure of the size of the space occupied by the geometric body.
The basic unit of measurement for volume is cubic metre, labeled with 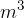 .
.
In addition to the basic, we also know larger and smaller units of volume. The most commonly used are shown in the following table:
The blue text in the table above represents the destinal prefix. Each prefix represents a certain power of 10 with an integer exponent, by which we must multiply the base unit to obtain a unit with this prefix. Since in the case of area, we use the square of the basic unit of measurement for length on the surface, the prefix is also cubed.
The following table can be used to convert between volume units:
In the first row of the table we write the volume in the given unit of measurement, and from the second row we read the same volume in the searched unit of measure.
Let's look at the use of the table in the following examples:
Volume is not usually measured, but calculated on the basis of measuring length and using mathematical equations.
The actual volume measurement can be performed by dividing into unit cubes (with edge length equal to one unit) and counting these cubes, but the method is not accurate and its interpretation goes beyond the content of the textbook.
A plane angle is a part of a plane bounded by two lines with the same starting point. You can read more about plane angles in the chapter Geometry in the plane - basic concepts.
In addition to the planes, we also know spatial angles, but their treatment exceeds the content of the subject matter, so they are not covered in this textbook. Therefore, we will use the simple term “angle” below, keeping in mind, the plane angle.
Angles can be measured in degrees or radians. In the first case, the basic unit is angular degree, and in the second, radian.
The basic unit of measurement for measuring plane angles in degrees is angular degree denoted with "°".
One angular degree represents an angle of size 1/360 of a full angle. The full angle therefore measures 360°.
In addition to the basic unit, we also have two smaller measuring units for angles. They are shown in the following table:
The units of measurement for angles, unlike the units discussed so far, do not differ by a factor of 10, but by a factor of 60.
The conversion between units of measurement for plane angles in degrees is best illustrated by the following examples:
The basic (and also the only) unit of measurement for measuring plane angles in radians is radian denoted as "rad".
Radian is a unit without dimensions, so we don't usually write it.
The angle measured in radians is defined by the centre angle.
The central angle with the base unit radian is equal to the ratio between the length of the corresponding circular arc and the radius of the circle:
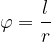
From the above equation, we come to two conclusions:
First, we assume that the length of a circular arc is equal to the total circumference of the circle:
Finding 1: Full angle measures 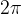 radians.
radians.
Now suppose that the length of a circular arc is equal to the radius of the circle:
Finding 2: One radian is the center angle belonging to such a circular arc that is equal in size to the radius of the circle.
Some mathematical problems are easier to solve with angles given in angular degrees and others with angles given in radians, we simply convert angles from one unit of measurement to another and vice versa.
We derive the equation for the conversion from degrees to radians. Let's start from the fact that the solid angle measures 360° in angular degrees, and in radians, 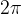 :
:
It follows from the above equation:
For conversion from angular degrees to radians, the angle size must be multiplied by 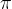 and divided by 180.
and divided by 180.
Now let us derive the equation in the opposite direction. Again, let us start from the fact that the solid angle measures 360° in angular degrees and 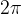 in radians:
in radians:
According to the above equation, we can write:
The conversion from radians to angular degrees requires us to multiply the size of the angle by 180° and divide by 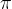 .
.
The following table lists the most commonly used angles in geometry, given in angular degrees and radians:
The connection between degrees and radians is also nicely visible on the unit circle.
A unit circle is a circle that has:
centre in the coordinate origin
radius of one unit (hence the name "unit")
The angles on the unit circle are shown as follows:
the top of the angle is in the coordinate origin
one arm of the angle is fixed to the positive part of the abscissa
the second arm of the angle rotates in the mathematically positive direction for the angle value
The following figures show acute, obtuse and reflex angles on the unit circle:
Once again, we write the definition of the angle in radians:
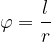
when
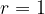
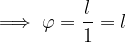
In a unit circle, the angle 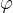 in radians is equal to the length of the circular arc.
in radians is equal to the length of the circular arc.
The figures below show the relationship between angular degrees and radians for the most special angles.
For more information on the unit circle and its use, see Trigonometry.
The coordinate system is presented in the chapter Rectangular coordinate system.