Personal collections
A company sells bags of pasta. The masses of large bags of pasta are normally distributed with mean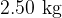 
and standard deviation 
.
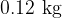Find the probability that the mass of pasta in a randomly chosen large bag is less than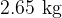 
.
A restaurant manager buys 160 of these large bags of pasta. Find the number of bags for which you would expect the mass of pasta to be more than 1.65 standard deviations above the mean.
The masses of small bags of pasta sold by the company are normally distributed with mean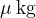 
and standard deviation 
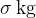. Tests show that 
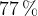of these bags have masses greater than 
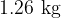, and 
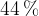have masses less than 
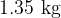. Find, in either order, the value of 
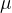and the value of 
.
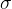or 
.
