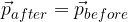Personal collections


Let's imagine a soccer player who intercepts the ball and redirects it towards the goal (see Figure 1).
He acts on the ball with force 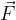 , but it lasts for a short time
, but it lasts for a short time  . This is the time the ball is in contact with the footballer's foot. The product of force and time is called the force impulse:
. This is the time the ball is in contact with the footballer's foot. The product of force and time is called the force impulse:
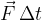
With a burst of force, he diverts the ball towards the goal. He changes the direction and speed of the ball. We say that he changes its momentum.
It would be more difficult for the soccer player to change the direction and speed of the ball if it were a medicine ball. It also makes a difference to a soccer player whether he kicks a medicine ball that moves slowly or quickly. These experiences help us to understand the momentum itself: the greater the mass of the body and the greater its speed, the greater its momentum:
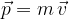
Momentum is also a vector. It has its own magnitude (which is equal to the product of mass and velocity) and also direction. It has the same direction as the velocity vector. When adding (or subtracting), the same rules of calculation with vectors apply to momentum, as we learned in the chapter Force as a vector, or in more mathematical material, where we discuss calculation operations between vectors.
A force impulse and a change in momentum are closely related and derived from Newton's second law. Let's take a closer look at this relationship.
A body with mass 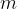 is acted upon by a force
is acted upon by a force 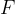 . The body begins to move with uniform acceleration
. The body begins to move with uniform acceleration 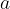 :
:
Also through the equations, we found out what we already suspected in the introduction: the impulse of force (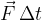 ) is the one that causes the body to change its momentum (
) is the one that causes the body to change its momentum ( ). We illustrate this graphically in Figure 2 below:
). We illustrate this graphically in Figure 2 below:
A force impulse is equal to a change in momentum:
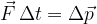
The change in momentum is given as:
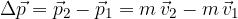
where 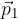 is the momentum before the impact of the force and
is the momentum before the impact of the force and 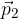 is the momentum after the impact of the force.
is the momentum after the impact of the force.
The law of conservation of momentum states that momentum is conserved if the sum of all impulses of forces acting on a body is zero. It is conserved even if the bodies collide with each other.
But let's look at the conservation law in a little more detail. Let's first discuss the following:
types of collisions between particles;
the difference between internal and external impulses of forces (collisions).
Let's imagine 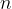 bodies in a confined space. Each body has its own momentum
bodies in a confined space. Each body has its own momentum 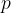 . During motion, the bodies touch each other, we say they collide. Collisions between bodies can be:
. During motion, the bodies touch each other, we say they collide. Collisions between bodies can be:
elastic
inelastic
partially elastic.
Let's take a look at them.
An elastic collision (also called an ideal collision) is a collision in which the entire kinetic energy is considered to be conserved during the collision.
An inelastic collision is a collision in which it is considered that the bodies stick together after collision. The kinetic energy of colliding bodies is not conserved.
In nature, however, collisions are never completely elastic. Let's take a ball and drop it from a certain height. If the ball were perfectly elastic, it would reach the same height as the height from which we dropped it after bouncing (disregarding air resistance). But the ball reaches a lower height after each bounce until it comes to rest on the ground. Such a collision is partially elastic since the ball does bounce, but with each bounce, some kinetic energy is converted into internal energy.
For comparison, let's take a plasticine ball. If you dropped it on the ground, it wouldn't bounce at all. The collision of the plasticine ball with the ground would be inelastic.
Let's go back to the billiards example. In order to be able to determine what is an internal and what is an external force impulse, we must first determine what a system is. The choice of system is completely arbitrary, usually, we choose the system in such a way that it is easiest for us to calculate or observe something happening.
In the case of billiards, we choose billiard balls for the system. Now that we have determined the system, we can determine the external and internal forces:
an external force impulse is anything that acts on the selected system from the outside. Let's list a few such external impulses of force:
We hit one of the balls with the stick: the hit with the stick is counted as an external impulse of force on the system. The rod is not part of our chosen system and by hitting the balls, we change the momentum. If the balls before the hit are stationary, now they are moving.
The ball bounces off the edge. The edge is not part of our system, so the action of the edge on the ball is also an external force impulse on the system. Even in the ideal case, when the collision with the edge is elastic, the direction of the momentum changes.
The frictional force between the ball and the base is also considered as an external force impulse. The base is not part of our system, but it causes a frictional force that reduces the total momentum.
however, an internal force impulse is everything that happens inside the system. For example, we count the collision between two balls as an internal impulse of force, since both balls are part of our chosen system.
Let's take a closer look at the internal force impulse. Let one ball collide with another:
When the first ball with mass 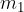 and velocity
and velocity  collides with the second (see Figure 5), which is at rest, it changes its momentum with a force impulse:
collides with the second (see Figure 5), which is at rest, it changes its momentum with a force impulse:
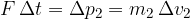
Due to the mutual interaction of forces, the second ball also acts on the first with the same and oppositely directed impulse of force:
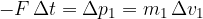
If we add both equations, we get:

We can see that the momentum of each ball has changed, but the total momentum has not changed.
External impulses of force change the total momentum of bodies. With this, they are distinguished from the internal impulses of forces that act during collisions. These change the momentum of individual bodies within the system, while the vector sum of all momentum remains unchanged.
We enclose several moving bodies in space and let them collide with each other. As a result of collisions, the directions and speeds of motion of individual bodies change. During collisions, impulses of force act on individual bodies, which change the speed and direction of motion of the body. But such impulses occur inside a closed space (within the system), so we call them internal impulses.
Let's write down the law of conservation of momentum: if no impulse of force acts on the bodies from the outside, the total momentum of all bodies in the system is conserved. The number, size, and type of internal collisions and forces are not important:

Let's demonstrate the momentum conservation law on the example of an inelastic collision of two bodies. Since in this case, both bodies represent a system, the collision between them is internal and therefore no external force acts on the system. What are the initial momentum  before collision and the final momentum
before collision and the final momentum 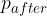 after collision?
after collision?
Let's write equation (1) again:
If there is no external force acting on the system of moving bodies, the total momentum is conserved. The total momentum of all bodies after the collision is equal to the momentum before the collision: