A mathematical expression (also called an algebraic expression) is a notation that can consist of numbers or variables which are usually denoted by lowercase letters.
The arithmetic operations and the functions take place between the expressions. Usually the order of the operations is determined by parentheses.
The expression is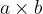 
is the same as 
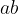. The multiplication sign can be omitted.
When an expression is multiplied by any number n or variable a, we get the n-th or a-th multiple of this term.
The variable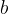 
is a multiple of the variable 
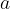if it can be written as:
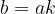
where k is any natural (or whole) number.
Multiples of the variable 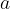are obtained by multiplying the variable 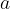by natural (or integer) numbers:
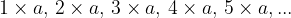
The set of all multiples of a is denoted by:
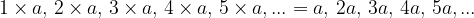
A monomial is a term that consists:
only of one number or one variable or of
numbers and variables multiplied together.
Expressions with addition or subtraction of multiple monomials can be shortened by adding together similar terms (we also call them like terms).
Monomials can be added together only if monomials are similar. That means they are only numbers or they have the same variables. We can also call monomial term.
A binomial is an expression that consist of two monomials that are added together or subtracted, but the monomials are not similar and for that they can not be added together.
Multinomials are expressions with two or more monomials.
Each of us has broken something into pieces that could not be dismembered into smaller ones; this type of separation is called prime factorization in mathematics. To break an expression means to write the expression as a product of factors that cannot be further broken down.
Each natural number can be divided into prime factors (prime numbers) in a single way or written as a product of prime numbers:
Splitting of the natural number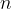 
into prime factors (prime numbers):
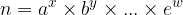
where 
are prime numbers;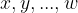 
are exponents that are natural numbers.
We calculate expressions by first removing the parentheses, taking into account the order of arithmetic operations. Namely, multiplication takes precedence over addition and subtraction, and we must pay special attention to the sign before the parentheses. If we have a minus sign before a parentheses, all the terms in the parentheses change signs. We use certain formulae to factorise expressions.
The square of the sum of two terms:
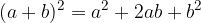
Here a binomial is squared.
The square of the difference of two terms:
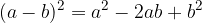
Here a binomial is squared.
The cube of a binomial when two terms are added:
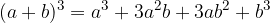
Here a binomial is cubed.
The cube of a difference of two terms:
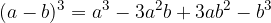
The difference of squares:
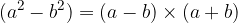
The difference of cubes:
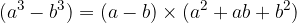
The sum of cubes:
Difference ofnth power can be factorised:
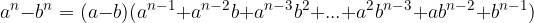
Here n is a natural number.
Splitting of a square trinomial:
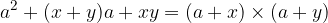
Here a trinomial means an expression in which three terms occur.
To expose a common factor means to write in parentheses the numbers that all the terms have in common. What is left of the individual numbers is written in the parentheses.
When finding common factors, it is always a good to do a test by multiplying the expression in parentheses with the exposed factor. If we get the initial expression, we have correctly found the common factors.
Now let's take a look at an example in which in addition to variables we also have numbers.
