Natural numbers are the numbers we count with. The set of natural numbers is denoted by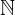 
and consists of numbers from one to infinity, which is denoted as
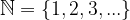
Properties of natural numbers are:
natural numbers are infinitely many
1 is a natural number
every natural number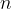 
has a successor 
two different natural numbers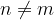 
have different successors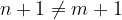 
1 is not the successor of any natural number
We choose the starting point and unit - mark the starting point with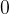 
and one unit in the right number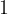 
one unit to the right of the number 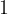we get the number 
we repeat the procedure by evenly applying the unit to the right to obtain the remaining numbers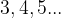 
Addition and multiplication operations are defined in the set of natural numbers.
Any two natural numbers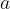 
and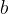 
add up and get the sum of 
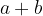, where the numbers 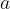and 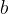are called the addends, and 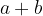the sum.
Arbitrary two natural numbers 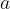and 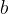are multiplied to give a product 
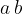, where the numbers 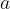and 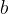are called the factors and 
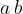the product.
When calculating with natural numbers, we must take into account the order of operations (multiplication takes precedence over addition) and parentheses, and in addition, certain laws apply to calculating with natural numbers.
The result is independent of the order of addition or multiplication.
Commutative summation:
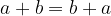
Multiplicity commutation:
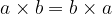
The result is independent of the order in which the factors are combined.
Addition associativity:
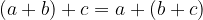
Multiplicative associativity:
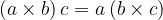
It connects multiplication and addition of natural numbers.
Distributive law:
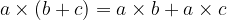
When multiplied by 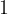, the result does not change.
Neutral multiplication element:
A prime number is a natural number that has exactly two divisors 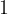and itself. All other natural numbers that have more than two divisors are called composite numbers. The exception is the number 1, which has only one divisor, so it is not a compound or a prime number.
Each natural number can be divided into prime factors (prime numbers) in a single way or written as a product of powers with prime numbers:
Split of natural number n into prime factors (prime numbers):
where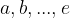 
are prime numbers; 
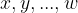and exponents that are natural numbers.
To factorize or highlight the common factor means to write in parentheses the most factor that all the terms have in common. The numbers are first split into the product of prime factors (prime numbers). The factors contained in all the terms are written outside parentheses, and everything that is left of the terms is written in parentheses.
