Personal collections


In the material, Uniformly accelerated motion, we learned that the speed of a body changes with acceleration or deceleration. But what is the cause of acceleration and deceleration?
What causes the change in the speed or direction of a body is the force acting on it.
In the above example, the soccer player, with the force of his legs, acted on the soccer ball. Let's imagine replacing the soccer ball with a heavy medicine ball. In this case, the soccer player would have to use a greater force on the ball to set it in motion.
In the following, we will learn how the physical quantities listed below are related to each other:
the mass of the body,
the force acting on the body, and
the acceleration of the body.
Here we will consider the motion where the force acts in the same or in the opposite direction to the motion of the body.
Let's take a trolley with mass 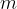 , which can move without friction on a horizontal surface, as shown in the figure below. We stand against the trolley and push it in front of us with a constant force
, which can move without friction on a horizontal surface, as shown in the figure below. We stand against the trolley and push it in front of us with a constant force  . The trolley moves uniformly accelerated with acceleration
. The trolley moves uniformly accelerated with acceleration  .
.
Now, we load the trolley with a load so that the total mass of the trolley and the load is twice as large, i.e.  . By measuring the force, we find out that we have to push the trolley with twice the force, i.e. with a force
. By measuring the force, we find out that we have to push the trolley with twice the force, i.e. with a force 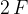 so that the trolley moves with the same acceleration.
so that the trolley moves with the same acceleration.
With twice the mass, we need twice the force for the same acceleration. Let's state the result in another way. The acceleration of a body is:
greater if a greater force is applied - acceleration is directly proportional to the force,
smaller if the body has higher mass - acceleration is inversely proportional to mass.
Let's write down the conclusion in mathematical form:
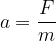
Let's check the accuracy of the above equation. Let's take twice the mass and denote it as 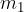 and twice the force denoted as
and twice the force denoted as  :
:
We see that the acceleration of the body does not change if we simultaneously double the:
mass and
force.
Let's rearrange the formula for the acceleration by making the force  the subject.
the subject.
The formula:
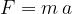
represents Newton's second law. If we translate it into words, it can be understood as follows: A body with mass 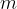 moves uniformly accelerated with acceleration
moves uniformly accelerated with acceleration  if the resultant force
if the resultant force  act on it.
act on it.
Using the above equation, we can express the unit for force using basic units of measurement. We do this by inserting units for individual quantities into the equation:
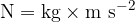
The resultant of the forces can be:
positive
A positive resultant means that it acts in the same direction as the motion of the body. In this case, the body moves with uniform acceleration (acceleration is positive).
negative
A negative resultant means the action of the force is in the opposite direction to the motion of the body. In this case, the acceleration is also negative. The motion is steadily decreasing.
Newton's second law reads:
Let the resultant of all the forces acting on a body with mass 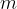 be equal to
be equal to  . Then the body moves uniformly accelerated with acceleration
. Then the body moves uniformly accelerated with acceleration  . This is mathematically expressed as:
. This is mathematically expressed as:
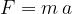
A positive force acts in the direction of motion and accelerates the body while a negative force acts in the opposite direction to the motion and slows the body down.
Let's look at some examples where a force acts in the direction of the motion of a body. The force is positive and accelerates the body.
Let's look at the example where we calculate the acceleration of a car.
If a force acts in the opposite direction to the motion of a body, the body moves uniformly decelerating. Let's look at a few examples of decelerating motion.
Let's look at an example in which we calculate the braking force.
Gravity is the force with which the Earth attracts all objects. The phenomenon is called weight or gravity.
Gravity acts not only on Earth but also on other celestial bodies. The Sun, the planets, and their moons have a gravity that is different from that on Earth.
The force of gravity will be denoted by 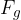 . The subscript
. The subscript 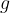 stands for gravity.
stands for gravity.
In the material, Free fall, we saw that a body moves with uniform acceleration during free fall. The acceleration of a body in free fall is called free fall acceleration or gravitational acceleration and we gave it the symbol 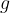 . It is approximately:
. It is approximately:
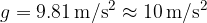
According to Newton's second law, weight can also cause a body to move.
Let's write Newton's second law:
We have obtained a version of Newton's second law for the weight of bodies. Weight is therefore equal to the product of mass and acceleration of free fall. Since the acceleration of free fall is approximately 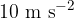 , we can say that the weight in Newtons
, we can say that the weight in Newtons 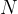 is numerically ten times the mass in
is numerically ten times the mass in 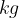 .
.
Weight or gravitational force 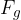 is the force with which the Earth (or another celestial body) attracts all bodies. We calculate it as the product of mass
is the force with which the Earth (or another celestial body) attracts all bodies. We calculate it as the product of mass 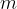 and gravitational acceleration
and gravitational acceleration 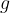 :
:
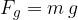
Let's look at how weight affects bodies:
at rest,
in free fall,
on a slope.
We will see that the motion of a body depends only on the base due to its weight.
For a body to be at rest, the resultant of all forces acting on the body must be equal to zero. If the weight 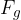 acts vertically downward, there must also be an equally large force acting vertically upward. This is the force with which the surface acts on the body. We call it the normal force and is denoted by
acts vertically downward, there must also be an equally large force acting vertically upward. This is the force with which the surface acts on the body. We call it the normal force and is denoted by 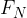 .
.
If the normal force is less than the weight of the body, the body moves in the direction of their resultant, i.e. vertically downwards.
However, if the force of the ground is zero (no ground or base), the body falls freely. Its motion is uniformly accelerated with an acceleration 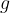 .
.
Let's place a body on a slope and see what kind of motion is caused by the weight of the body alone. The weight acts vertically downwards, towards the centre of the Earth. Let's resolve it into two perpendicular components:
the static component, and
the dynamic component.
The static component 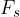 of the weight acts perpendicular to the slope and presses the body against the slope. The slope, on the other hand, acts on the body with an opposite equal force
of the weight acts perpendicular to the slope and presses the body against the slope. The slope, on the other hand, acts on the body with an opposite equal force 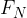 . The forces
. The forces 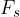 and
and 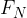 are in equilibrium (they cancel each other out), so the body does not move in a direction perpendicular to the slope.
are in equilibrium (they cancel each other out), so the body does not move in a direction perpendicular to the slope.
The dynamic component 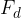 of the weight acts along the slope. If no other external forces act on the body (friction, resistance, pulling, and pushing forces), then
of the weight acts along the slope. If no other external forces act on the body (friction, resistance, pulling, and pushing forces), then 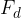 is the resultant of all the forces acting on the body. Therefore, according to Newton's second law, it causes the body to move with uniform acceleration down the slope. The steeper the slope, the greater the dynamic component and the greater the acceleration.
is the resultant of all the forces acting on the body. Therefore, according to Newton's second law, it causes the body to move with uniform acceleration down the slope. The steeper the slope, the greater the dynamic component and the greater the acceleration.
The slope can be imagined as a gentle free fall. In the extreme case, if the slope is vertical, the motion turns into a free fall.