Personal collections


The interaction of forces is present everywhere. If we push our hands against the wall of the house, we feel that the wall also acts back on our hands. The Earth attracts an apple fruit hanging from the tree with the force of gravity, but the apple fruit also attracts the Earth. Bodies act on each other - mutually.
Forces can interact:
in contact. For example, a pencil lies on a table. It presses down on the table with its weight, but at the same time, the table presses back on the pencil.
far away. For example, the Sun acts on planets that are far away from it. It acts on the planets with the same force as the planets act back on the Sun.
This is the law of interaction of forces, also known as Newton's third law of motion. If we summarize Newton's third law briefly, it says: action equals reaction.
With the help of the law of mutual interaction of forces, we can also explain internal forces. Let's look at an example.
Let’s take a closer look at the phenomena we just described.
Newton's third law says that forces act mutually. The easiest way to understand the effect of the interaction of forces is through examples.
According to the examples above, we learn about the laws of the interaction of forces, also known as Newton's third law. Bodies always interact with each other. This action can be through a mutual contact or even at a distance.
The law of interaction of forces or Newton's third law states that bodies act on each other mutually. If the first body acts on the second with a force 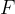 , the second body will act on the first with an opposite force
, the second body will act on the first with an opposite force 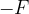 .
.
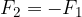
Let's take a cord on which a block is hung. The cord is attached to the ceiling. The weight 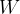 of the block acts downward. At the point where the cord is attached to the ceiling, an opposite force to the weight of the block acts and is directed upwards. Let's call it the ceiling force (tension)
of the block acts downward. At the point where the cord is attached to the ceiling, an opposite force to the weight of the block acts and is directed upwards. Let's call it the ceiling force (tension)  .
.
We notice that the cord is stretched, from which we conclude that forces are also acting in the cord. These are the opposing forces of gravity and the ceiling; because they act in the cord itself, we call it an internal force. Since the cord is at rest, the two internal forces are in equilibrium (their resultant is zero).
The same applies to all constructions. Take, for example, a bridge. If the bridge is stable, the sum of the forces at each point of the bridge is zero, even if several forces act at the observed point.
Knowledge of the internal forces in structures is important because this helps us to understand what kind of loads they can withstand. For example: in addition to the basic load (e.g. the weight of the structure itself), the bridge must carry additional loads (e.g. a truck on the bridge). The structure must be such that the strength limit of the materials from which the structure is built is not exceeded at the maximum expected load.
Let's take an elastic spring and apply a force 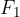 to it, as shown in Figure 4 below:
to it, as shown in Figure 4 below:
The spring stretches until the sum of the internal forces in the spring is zero. Then the stretching stops and the force 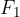 on the spring is equal to the tensile force
on the spring is equal to the tensile force 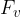 in the string:
in the string:
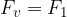
Equilibrium is established at an extension 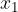 . Through measurements, we find that the magnitude of the pulling force
. Through measurements, we find that the magnitude of the pulling force 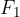 is directly proportional to the extension
is directly proportional to the extension 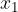 of the spring:
of the spring:

How much this extension will be at a certain force also depends on the hardness of the spring: with a softer spring, the extension will be greater for the same force. The proportionality constant between the force 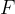 and the extension
and the extension 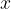 is denoted by
is denoted by 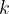 and is called the force or spring constant. The equation is then written in general form, as:
and is called the force or spring constant. The equation is then written in general form, as:

The written equation is called Hooke's law. We also express the force constant 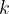 from Hooke's law, as:
from Hooke's law, as:
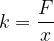
The unit for the force constant is 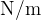 .
.
The force with which we act on an elastic rope or spring is equal to the force with which the spring resists the external force. Hooke's law applies:

where 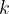 is the force constant representing the stiffness of the spring.
is the force constant representing the stiffness of the spring.
We use Hooke's law to measure forces using a spring balance. The spring balance can contain a spring on which a scale is drawn, and calibrated in 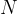 .
.
In Figure 5, on the left, we can see an unloaded spring. The spring balance in the figure has a measuring range of 0.1 to 1 N. The measuring marks, marked with a black line, are located at a distance of 0.1 N. We hang an object on the balance, Figure 5, right, and read the force of the weight of the object which is 0.5 N.