Personal collections


In the material, Magnetic field density, we learned how to calculate the magnetic field density inside a long and narrow coil through which a current flows. We assumed that the material inside the coil is air.
What if we insert some material into the coil? What is the magnetic field density then?
In the material, Electric field strength, we saw that matter in an electric field always reduces the electric field strength. However, if a substance is placed in a magnetic field, the magnetic field density can be weakened or strengthened.
For air or airless space, the relationship between the density 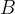 and the strength
and the strength 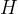 of the magnetic field is given as:
of the magnetic field is given as:
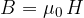
If a substance or material is inserted into the magnetic field of a coil, the density of the magnetic field in it weakens or strengthens. We must also take into account the magnetic property of this substance, which is called relative permeability 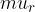 . The relative permeability factor is added to the above equation for the strength of the magnetic field in the substance:
. The relative permeability factor is added to the above equation for the strength of the magnetic field in the substance:

where:
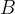 - magnetic field density
- magnetic field density
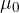 - permeability of free space
- permeability of free space
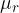 - relative permeability
- relative permeability
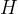 - magnetic field strength
- magnetic field strength
Based on the value of 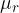 , substances are classified as:
, substances are classified as:
diamagnetic substances: 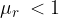 e.g. water, mercury, copper, carbon dioxide.
e.g. water, mercury, copper, carbon dioxide.
paramagnetic substances:  e.g. aluminum, zinc, lead, tungsten.
e.g. aluminum, zinc, lead, tungsten.
ferromagnetic substances: 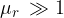 e.g. iron, cobalt, nickel.
e.g. iron, cobalt, nickel.
The relative permeability factor 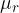 has no unit and defines;
has no unit and defines;
how many times the density 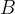 of the magnetic field in a substance weakens or strengthens
of the magnetic field in a substance weakens or strengthens
compared to the density 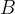 in the free space.
in the free space.
In a vacuum, the relative permeability is equal to 1. According to the above values of  , we see that diamagnetic substances slightly weaken the magnetic field density. Paramagnetic substances slightly increase the magnetic field density. Ferromagnetic substances greatly strengthen it.
, we see that diamagnetic substances slightly weaken the magnetic field density. Paramagnetic substances slightly increase the magnetic field density. Ferromagnetic substances greatly strengthen it.
In this material, we will focus on ferromagnetic substances.
If we look at a slice of ferromagnetic material under a microscope, we notice individual areas of grains. We call them Weiss or magnetic domains. The characteristic of these domains is that each domain has its own magnetic field, only that they are oriented differently and cancel out on the outside - bottom left image.
Under the influence of an external magnetic field, the fields of the magnetic domains are oriented in such a way that they amplify the external magnetic field - picture on the right. The total magnetic field density increases.
Let's take a flat air coil:
Let's plot the graph of the magnetic field density 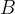 against the magnetic field strength
against the magnetic field strength inside the coil. The magnetic field density
inside the coil. The magnetic field density 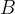 is obtained by multiplying
is obtained by multiplying 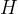 by the permeability of free space
by the permeability of free space 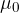 - the blue line in the figure below.
- the blue line in the figure below.
Now we insert a ferromagnetic core in the middle of the coil - the red curve in the picture above. Increasing the current through the coil also increases the magnetic field strength inside the coil. The elementary agents in the magnetic domains in the core begin to align in a direction such that their magnetic field additionally strengthens the external magnetic field. The magnetic field density 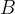 increases steeply - the left, steep part of the red curve.
increases steeply - the left, steep part of the red curve.
This happens until all the elementary magnets in the magnetic domains point in the direction of the external magnetic field - the right, flatter part of the red curve. Now the contribution of the elementary magnets is constant. We say that the ferromagnetic core is in saturation.
The relative permeability therefore tells how many times the magnetic field is amplified by the orientation of the magnetic domains. The relative permeability is not constant but rather depends on the strength 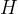 of the magnetic field. Therefore, in most cases, it cannot be given as a numerical value but rather it can be read from the magnetization curve of the selected ferromagnetic material.
of the magnetic field. Therefore, in most cases, it cannot be given as a numerical value but rather it can be read from the magnetization curve of the selected ferromagnetic material.
The permeability 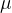 of a material depends on both the relative permeability
of a material depends on both the relative permeability  and the permeability
and the permeability 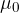 of a vacuum, and is given by as :
of a vacuum, and is given by as :
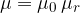
It is worth noting that a ferromagnetic material loses its relative permeability (drops to one) if the material is heated sufficiently. The temperature at which this happens is called the Curie temperature. The Curie temperatures for the three most common ferromagnetic material are in the table below:
Relative permeability tells how many times the magnetic field density in a ferromagnetic substance is amplified, compared to the magnetic field density in air or vacuum. It depends on the strength of the magnetic field and can be read from the given magnetization curve.
The permeability 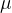 of a material depends on both the relative permeability
of a material depends on both the relative permeability  and the permeability
and the permeability 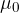 of a vacuum, and is given by as :
of a vacuum, and is given by as :
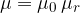
The magnetic field density 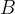 in a material is given as:
in a material is given as:

The magnetic field density 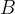 in a long and narrow coil with a ferromagnetic core can be calculated using the formula:
in a long and narrow coil with a ferromagnetic core can be calculated using the formula:
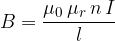
The graph above refers to the first magnetization of the ferromagnetic core. If we then lower the magnetic field strength, the magnetic field density no longer follows the first magnetization. The elemental magnets in the magnetic domains more or less remain still oriented in such a way as to strengthen the external magnetic field. What happens is that the core remains magnetized even though the magnetic field strength has dropped to zero. This is called remanent or residual magnetism, in the figure below it is marked with 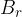 . It can be canceled out by reversing the direction of the current and thus of the external magnetic field to the value
. It can be canceled out by reversing the direction of the current and thus of the external magnetic field to the value  . This is the coercive magnetic field strength.
. This is the coercive magnetic field strength.
Similarly, we only get a curve shifted to the right if the magnetic field strength increases again - see the right curve in the two images below.
The curve we got is called hysteresis or hysteresis loop. In the image on the left, the hysteresis is wide with a large residual magnetism. Material that has such hysteresis can be used to record sound or data to disk. This material "remembers" that it was magnetized and remains magnetized. It is called a hard ferromagnetic material.
In the image on the right, the hysteresis is narrow. It is obtained by choosing a soft ferromagnetic material. It is used e.g. for cores of transformers, electric motors, electromagnets for lifting loads, etc. Here we want the hysteresis to be very narrow, ideally a single curve.