We compute complex numbers according to the rules for computing with polynomials, by:
treating the imaginary unit i like any other algebraic quantity and
we consider the values of the individual powers of the imaginary unit i.
When calculating, especially when multiplying and finding the powers complex numbers, we obtain the powers of the imaginary unit i, so we will first look at their values and then the computational operations between complex numbers.
When exponenting an imaginary unit, we take into account that for any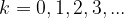 
:
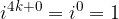
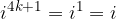
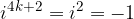
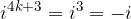
We see that to calculate the power of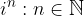 
, we must divide the number n by four and that the value of the power is determined by the remainder of this division.
Let's look at a concrete example of calculating the power of an imaginary unit:
The sum or difference of complex numbers is a complex number whose real component is the sum or difference of their real components, and the imaginary component is the sum or difference of their imaginary components.
Let's look at the addition or subtraction of complex numbers in a concrete case:
Complex numbers are multiplied by the rules of multiplication of polynomials.
Complex numbers are raised to powers using the forms for the square and cube of binomials:
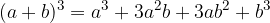
Addition, subtraction, multiplication and powers of complex numbers are subject to the usual calculation rules of addition, subtraction, multiplication and powers of polynomials.
Let's look at an example in which different arithmetic operations occur:
Two complex numbers are exactly the same when their real components and also their imaginary components are the equal.
Let's look at an example of using the definition of equality of complex numbers:
