In this material, we will look at basic arithmetic operations with fractions. These are:
addition
subtraction
multiplication
division
Then we will look at everything we can do with fractions, provided that it does not change its value. By this we mean in particular:
expanding fractions and
reducing fractions.
Each of the above actions will be considered separately:
The principle of summing fractions is divided into two points, according to the denominator.
Fractions have the same denominator
If the fractions have the same denominator, we add them by adding only their numerators and overwriting the denominator. So:
Fractions have a different denominator
If the fractions have different denominators, we must first extend them to a common denominator. So:
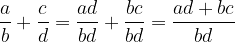
The following two laws apply to the summation of fractions:
Commutativity is the law of replacement. So, addition of fractions is commutative:
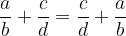
Associativity is the law of association. Addition is an associative operation, so:
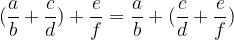
Subtraction is similar to addition. So here, too, we will divide it into two points, separated by a denominator.
Fractions have the same denominator
If the fractions have the same denominator, subtract them by subtracting only their numerators and overwriting the denominator. So:
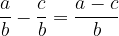
Fractions have different denominators
If the fractions have different denominators, we must first extend them to a common denominator. So:
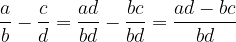
Multiply the fraction by multiplying both numerators by each other and both denominators by each other. So:
The following three laws apply to the multiplication of fractions:
Commutativity is the law of replacement. So the multiplication of two fractions is commutative when:
Associativity is the law of association. Multiplication is an associative operation, so:
Addition and multiplication of fractions are connected by the law on distributivity or the law on breakdown:
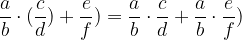
In order to be able to define the division of fractions, we must first explain what the inverse value of a fraction is.
The inverse of a fraction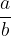 
, where a and b are non-zero, is the fraction 
.
Formally, we write this as:
The inverse of the fraction 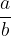is defined as:
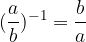
The product of a given and its inverse fraction is equal to 1. So:
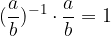
We can now define fraction division as:
Divide the fraction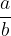 
by the nonzero fraction 
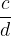(c other than 0) by multiplying the fraction 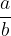by the inverse of the fraction :
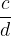Note: The division can also be written in the form of a double fraction:
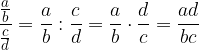
Expand the fraction by multiplying the numerator and denominator by the same non-zero number. The resulting fraction represents the same rational number as the original. So:
The fractions 
and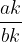 
are the same for a non-zero number k:
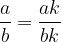
The fraction is shortened by dividing the numerator and denominator by any common divisor of these two numbers. The resulting fraction represents the same rational number as the original.
A fraction is reduced if the numerator and denominator are coprime. Each fraction is equivalent to exactly one reduced fraction with a positive denominator. To shorten a fraction, we simply need to divide the numerator and denominator by their greatest common divisor.
