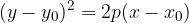Personal collections


A parabola is the set of all points T (x, y) in a plane that are equidistant from the directrix (v) and from the point F (focal point).
The geometric definition of a parabola can be written as:
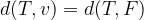
The distance between the focal point of the parabola (F) and the directrix is called the parameter of the parabola p.
The characteristics of a parable are most easily identified with the help of a sketch:
the marked characteristics on the sketch are:
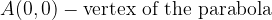
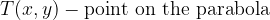
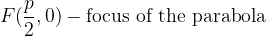
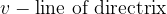

A parabola is a second-order curve, so the general equation for second-order curves also applies to it:
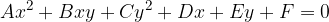
where 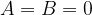 and the equation is transformed into:
and the equation is transformed into:
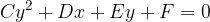
In fact, as we will find out later that it is a quadratic equation. This can also be seen by placing  in the general equation of the second-order curve; we get nothing but quadratic equation:
in the general equation of the second-order curve; we get nothing but quadratic equation:
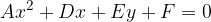
A parabola with a vertex whose coordinate is the origin is a parabola with vertices at the point A (0,0).
Let's look at a sketch of this parabola:
As we said in the introduction, a parabola is a set of points that satisfies the equation:
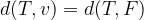
From the graph we can understand by comparing that 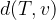 applies:
applies:
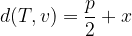
for 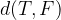 we use the simple formula for distance between points:
we use the simple formula for distance between points:
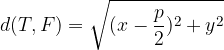
From what has been said, we can derive the equation of the parabola.
We derive the equation of parabola:
The equation of the parabola with vertex A (0,0) is:
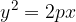
If the first parabola is mirrored over the y axis, we get the second form of the parabola. Let's look at a sketch of this parabola:
When mirroring across the y axis, x turns into its negative value: 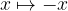 . We write the equation of the mirrored parabola:
. We write the equation of the mirrored parabola:
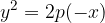
We remove the brackets and get the equation of the parabola:
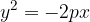
The equation of the parabola mirrored across the y axis and with the vertex A (0,0) is:
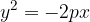
If we rotate the first parabola by an angle 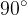 , we get a new form of the parabola. In this case, the parabola is also a graph of a quadratic function.
, we get a new form of the parabola. In this case, the parabola is also a graph of a quadratic function.
We derive the equation of the parabola in this position with the help of the introductory definition of the parabola, which we already know from the introduction:
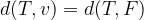
From the graph we can understand that 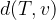 applies:
applies:
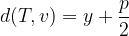
for 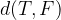 we use the simple formula for distance between points:
we use the simple formula for distance between points:
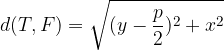
From what has been said, we can derive the equation of the parabola.
We derive the parabola equation:
The equation of the parabola rotated by 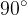 and with vertex A (0,0) is:
and with vertex A (0,0) is:
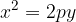
If we rotate the first parabola by an angle 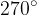 , we get a new form of the parabola. Even in this case, the parabola is a graph of a quadratic function.
, we get a new form of the parabola. Even in this case, the parabola is a graph of a quadratic function.
Note that in this case the parabola is the same as if the third form of the parabola were mirrored across the y axis or if 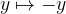 . We write the equation of the mirrored parabola:
. We write the equation of the mirrored parabola:
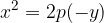
We remove the bracket and get the equation of the parabola:
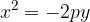
The equation of the parabola rotated by 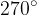 and with vertex A (0,0) is:
and with vertex A (0,0) is:
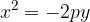
In case we move the parabola, every 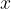 for
for 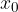 and every
and every 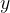 for
for 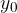 :
:
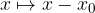
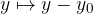
we get a parabola in a position away from the origin.
The characteristics are also marked on the sketch are:
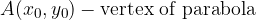
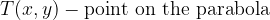
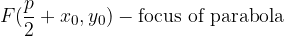
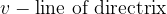

The equation of the displaced parabola and with the vertex in 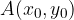 is:
is: