

The triangle is explained in more detail in the material Triangle. In this material, we will look at the role of the determinant in calculating the area of a triangle.
Let us define a triangle ABC in the plane of three (nonlinear) points A, B and C.
The perimeter of the triangle ABC is calculated by summing the distances between the points A and B between B and C and between C and A:
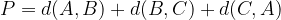
where d is the length of the line between two points, e.g.
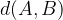
determines the length between the points A and B.
The area of a triangle in a plane is calculated using the determinant.
The determinant is generally written as
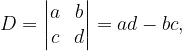
where a, b, c and d are any real numbers.
The determinant is important because it can be used to calculate the area of a triangle. Given three vertices of a triangle:
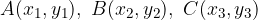
the area of the triangle is calculated according to the form:

where:

The area of the triangle is calculated using the form:
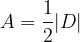
Triangle ABC is positively oriented if the vertices A, B and C follow counterclockwise and negatively oriented if the vertices follow clockwise.
If:
D> 0, the triangle is positively oriented;
D <0, the triangle is negatively oriented;
D = 0, points A, B and C lie on the same line.