A polynomial, usually denoted by p (x), is the final sum of a variable - usually denoted by x - which appears in the sum of different powers.
In mathematical language, a polynomial p (x) degrees n is defined as a real-valued function, given by the rule:
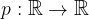
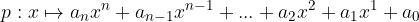
In general, we write the polynomial as follows:
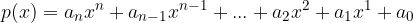
where 
real numbers, are called polynomial coefficients and valid:
n but is a natural number. The first and last terms have their names:
Leading coefficient: The coefficient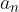 
is called the leading coefficient or leading term.
Constant term: coefficient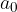 
is called a free term or constant term.
A polynomial that has all coefficients equal to zero is called a zero polynomial. The zero polynomial is:
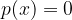
Domain and Range
In the definition of a polynomial, we mentioned that the polynomial is a real-valued function.
From the record 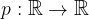and knowledge of the term real function, we understand that:
Domain is a set of real numbers,
Range is a subset of real numbers.
The domain and range can also be written with mathematical signs:
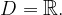
As well as Range:
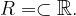
To calculate the value of a polynomial, we must have the value x given. When we have a given value x, we calculate the polynomial by inserting a value into the polynomial. Let's look at an example.
The value of the polynomial for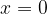 
is equal to the constant term of the polynomial.
The value of the polynomial for 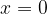and the zero of the polynomial are two different concepts.
The value of the polynomial for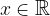 
can also be calculated using the Horner algorithm.
Polynomials are the same when they have the same value for each real number. However, in order not to calculate and compare the values of two polynomials for each real number, we will use the following theorem:
Two polynomials are equal only if they have the same degree and the same coefficients at powers of the same degree.
