Bodies that are raised have potential energy.
But how do bodies possess potential energy?
If we want a body to possess potential energy:
we have to raise it, or
it just needs to get to a higher position.
When we lift a body, we perform work on it. The work we do when lifting a body is stored in the form of the body's potential energy. If the body reaches the higher position by itself, the body does work on itself. We will learn more about energy conversions in the material Principle of kinetic and potential energy.
In the above examples, we have seen that the body’s potential energy increases with height. Let's take a look below:
how to determine the height of bodies and
which quantities still influence the determination of potential energy.
For all the bodies from the above examples, we can determine the height at which they are located. In order to be able to measure the height, we have to start measuring it from somewhere.
In the example above, we found that we need a starting point to measure the height. This starting point is called the zero height.
A zero height is one in which the height is zero.
When specifying the height, we must therefore always specify a zero height as well.
For the bodies we observe in physics, it does not (always) make sense to choose a zero height at sea level. We choose it most often:
on the ground where the body may fall,
or in the initial position of the body.
The height of the observed body is denoted by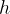 
. It indicates the shortest distance between:
the horizontal plane on which we chose the zero height, and
the position of the observed body.
Let's look at how we determine the height in the case of balls standing on rough terrain.
If we compare the heights of several bodies at the same time, we must choose the same zero height for all bodies.
The potential energy of a body is closely related to the choice of zero height. According to the agreement, it is valid that:
if the body is at zero height (i.e., not raised)
then its potential energy is zero.
However, if the body is:
raised, it has a positive height and potential energy;
lowered, it has a negative height and potential energy;
We learned that the potential energy of a body depends on its height. We also know from everyday life that it does not matter if we lift a heavy stone or a bird's feather from the ground. It is obvious that the feather is easier to lift, so we wonder if the weight also affects the potential energy of a body.
Let's answer the question with an example.
We found that (lifted) bodies with greater weight also have greater potential energy.
Through experiments, we find that the potential energy is directly proportional to the:
height and
weight of a body
Let's express the conclusion mathematically. We use the notation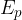 
for potential energy and the unit for measuring potential energy is the same as for work, the joule (
).
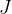The potential energy of an observed body is calculated as the product of the weight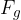 
of the body and the height 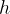at which the body is raised.
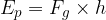
We note that the weight 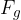is given as:
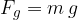
Therefore:
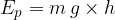
Using the above equation, we can calculate the potential energy of the bodies. Let's look at a simple example.
Height comes into the equation for potential energy. In the case with flowers (see above), however, we found that each observer can measure their own height. This means that each observer can calculate his own potential energy - and for one and the same body!
The potential energy depends on which zero height we choose.
We don't like it in physics that each observer can calculate his own potential energy for the same body. We want the same results - no matter who measures or calculates them. We do this by calculating the change in potential energy.
The height of the body depends on the selected zero height. But it is different if we observe the change in height. The change in height does not depend on the selected zero height. Let's look at an example:
The change in height is calculated as the difference between the:
final height,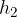 
and
initial height,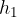 
.
We denote the change in height by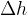 
and write it as:
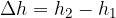
The Greek letter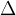 
is read delta and means change.
Interesting fact: We use a similar notation in other cases when we calculate the change of a quantity. In the same way, e.g. we also calculate the change in time or the change in speed when describing the motion of bodies.
We usually simplify the calculation if we choose the zero height correctly. Let's look at an example.
As with height, when we calculate the change in height instead of height, we also calculate its change in potential energy. This avoids the problem where each observer, due to a different choice of zero height, can calculate the potential energy of a body differently.
The change in potential energy does not depend on the choice of zero height. Therefore, it is precisely determined and calculated the same by every observer.
The change in potential energy is denoted as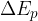 
.
The change in potential energy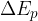 
is calculated as the product of body weight 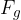and change in height :
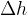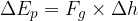
but:
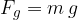
Therefore:
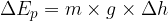
To calculate the change in potential energy, we observe only the initial and final positions of the body. The equation gives the difference in potential energy between the initial and final positions.
The path along which the body moves to the final position is not important for the calculation of the change in potential energy.
Let's look at an example.
In all the cases described so far, we have taken into account that the height is measured:
from zero height
to the lower point of the observed body.
Let’s look at an example where the above notion fails.
The potential energy of a body changes whenever the position of the body's centre of gravity changes.
A similar change in the position of the centre of gravity, as in the above example, is also represented by a body that is overturned. For all such bodies whose position of the centre of gravity changes, even though the lowest point on the body does not move, we must measure the height:
from zero height
to the centre of gravity of the body.
Let’s calculate the change in potential energy for such a body.
