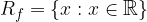A cube root function can be expressed as given below:
where the radicand, a(x), is an algebraic expression. In this material, we shall consider radicands of simple linear expressions.
Having identified a few examples of cube root functions, let's now look at evaluating them. To evaluate a cube root function f(x) we substitute the given values for x in the function.
Let's examine the graph of the basic cube root function:
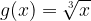
To have a good grasp of the cube root function, we need to be able to draw the graph of the function. This can be done accurately by evaluating the function for some values of x. The values are then tabulated and plotted as points on the graph. These points are joined together to form the curve of the function.
Now, let's tabulate the function g. We obtain the values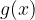 
of the function for some values of x.
We plot the graph of the function g:
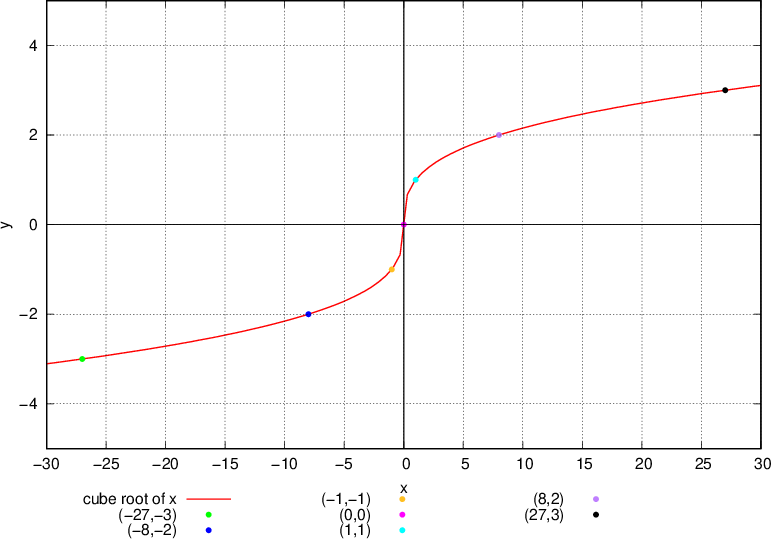
From the graph above, we can see that the curve covers:
the whole of the x axis and
the whole of the y axis.
The domain and range of a cube root function describe the region where the cube root function exist.
Here we shall discuss how the domain and range of the basic cube root function,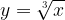 
, and generally other cube root functions, 
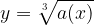, can be obtained graphically and numerically.
We will explore the properties and graphs of general and more complex radical functions in the material Radical Functions.
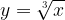
From the graph of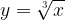 
drawn above, the following facts can be deduced about the domain and range of the basic cube root function.
Firstly, the domain of the basic cube root function 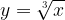is a set of all real numbers. Unlike by the square root functions, the radicand of the basic cube root function does not have any restrictions. For the function to exist, the radicand can be any real number.
Mathematically, the domain of the basic cube root function, denoted by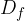 
, is written in the interval notation as:
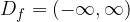
or in set notation as:
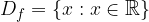
Secondly, the range of the basic cube root function, 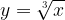, just like its domain, is a set of all real numbers (both negative and positive). This is because the cube roots of positive and negative real numbers exist, and are positive and negative real numbers, respectively.
Mathematically, the range of the basic cube root function, denoted by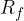 
, is written in the interval notation as:
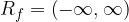
or in set notation as:
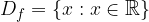
The domain of the basic cube root function 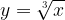is a set of all real numbers 
. This is written as:
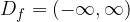
The range of the basic cube root function 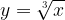is a set of all real numbers. This is written as:
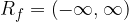
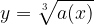
The domain of a cube root function can be obtained by graphical or numerical approaches.
Graphical Approach of Obtaining the Domain of a Cube Root Function
Graphically, the domain of a cube root function is the region of the x-axis covered by the function.
Numerical Approach of Obtaining the Domain of a Cube Root Function
Numerically, the domain of a cube root function is a set of x-values for which the function exist.
Observe that all real numbers have unique cube roots. Hence, the domain of a cube root function is a set of all real numbers.
The domain of any cube root function,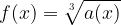 
, whose radicand 
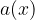is a linear expression, is a set of all real numbers 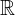. This is written in interval notation as:
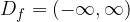
or in set notation as:
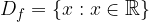
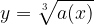
The range of a cube root function can be obtained by graphical or numerical approaches.
Graphical approach of obtaining the range of a cube root function
Graphically, the range of a cube root function is the region of the y-axis covered by the function.
Numerical Approach of Obtaining the Range of a Cube Root Function
Numerically, the range of a cube root function is a set of the values of the cube root function.
Observe that the cube roots of all real numbers are real numbers. Hence, the range of any real number is a set of all real numbers.
The range of any cube root function, 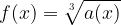, whose radicand 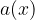is a linear expression is a set of all real numbers 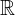. This is written in interval notation as:
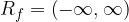
or in set notation as:
