Personal collections

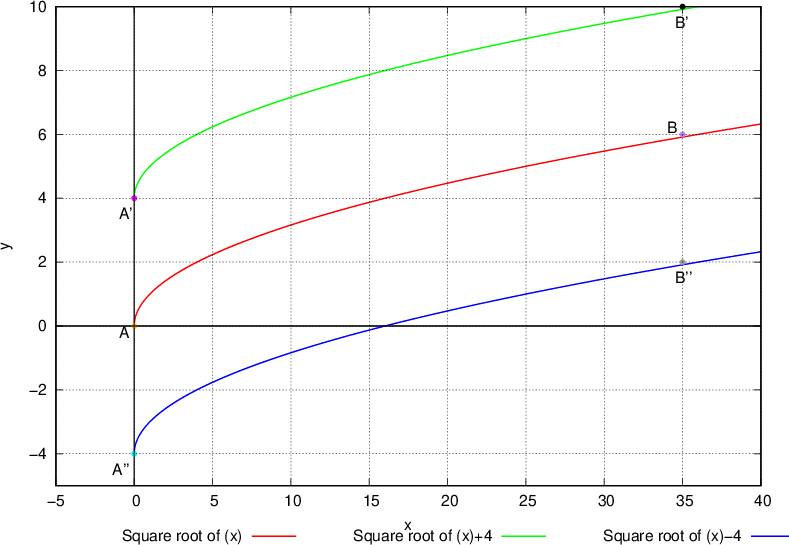
A radical function is described as pictured below:
where the index  can be any integer greater than 1: so 2, 3, 4 etc. And the radicands here shall be limited to linear expressions.
can be any integer greater than 1: so 2, 3, 4 etc. And the radicands here shall be limited to linear expressions.
For the two non-negative indexes 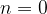 and
and 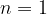 , such functions are not regarded as radical functions. Let's examine why they are not.
, such functions are not regarded as radical functions. Let's examine why they are not.
A radical function is generally written as:

And according to indices, the nth root of a number or an expression can also be written as an exponent:

Comparing the equations 1 and 2, a radical function can also be written as:
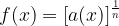
For 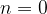
In other words, when 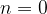 , such a radical function is undefined.
, such a radical function is undefined.
For 
We can see that the radical sign is not appearing anymore. Hence, we say f(x) is not a radical function but a linear function.
Having identified a few examples of radical functions, let's now look at evaluating them. To evaluate a radical function 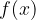 we substitute the given values for
we substitute the given values for 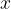 in the function.
in the function.
We shall firstly look at the graph of the basic radical functions. These shall be divided into two - even radicals and the odd radicals. Then we shall compare them with square root functions and cube root functions.
Radical functions whose indexes are even numbers are regarded as even radical functions. Examples of even radical functions include:

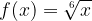
Let's examine the graphs of some basic even radical functions and compare them to observe any similarities or differences among them.
Radical functions whose indexes are odd numbers are regarded as odd radical functions. Examples of odd radical functions are:
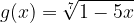
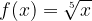
Let's examine the graphs of some basic odd radical functions and compare them to observe any similarities or differences among them.
In the earlier materials, we have discussed the domain and range of square root functions and the cube root functions. Now, we can generalise the concept for all other radical functions by subdividing them into even radical and odd radical functions.
From the graphs of the basic even radical functions drawn above, we have seen that these functions share the same properties as the square root functions. The similarity can be traced to the fact that they are all even roots. Hence, we say, all even radical functions have the same properties as the square root functions.
Domain of Even Radical Functions
Like the square root functions, the radicand of any even radical function cannot be negative for the function to exist. Hence, for any even radical functions, its domain is a set for which its radicands must be greater or equal to zero.
That is, the domain of any even radical function, 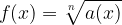 , is given by:
, is given by:
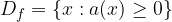
Range of Even Radical Functions
This is a set of values of an even radical function. It can be obtained by substituting the boundary values of the domain into the even root function.
For a basic even radical function, 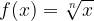 , the range is the set of all positive numbers including zero. This is written as:
, the range is the set of all positive numbers including zero. This is written as:
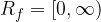
Radical functions whose indexes are odd numbers are regarded as odd radical functions. Examples include:
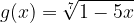
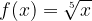
Domain of Odd Radical Functions
Like with the cube root functions, there is no restriction for the radicands of an odd radical function. Hence, for all odd radical functions whose radicands are linear expressions, the domain of any of such functions is the set of all real numbers. This is written in interval notation as:
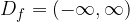
Range of Odd Radical Functions
This is the set of values of an even root function. It can be obtained by substituting the boundary values of the domain into the even root function. Similarly, for odd radical functions whose radicands are linear expressions, the range of any such functions is the set of all real numbers. This is written in interval notation as:
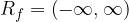
The domain and range of any basic even radical function, 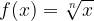 , is given by:
, is given by:
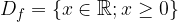
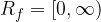
The domain and range of any basic odd radical function, 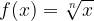 , is given by:
, is given by:
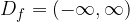
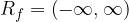
Transformation of radical functions could be explained by translation (shifting), reflection (flipping) or dilation (stretching or shrinking). Here, we shall look at the different forms by which a basic radical function, 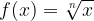 , can undergo transformation.
, can undergo transformation.
Here, the basic radical functions are transformed by adding or subtracting a real number c from it. We shall illustrate the forms by drawing their graphs on the same axes.
We tabulate the basic function 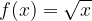 and the transformed functions
and the transformed functions 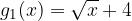 and
and  :
:
We plot the graph of the function 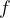 ,
,  and
and 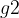 :
:
From the graph above, it can be seen that the red curve represent the basic radical function, 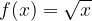 , the green and blue curves represent the transformed radical functions
, the green and blue curves represent the transformed radical functions 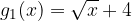 and
and  , respectively.
, respectively.
For example, points 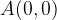 and
and 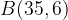 are shifted vertically upwards by 4 units each to points
are shifted vertically upwards by 4 units each to points 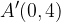 and
and  , respectively to produce the green curve. Furthermore, points
, respectively to produce the green curve. Furthermore, points 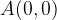 and
and 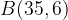 are shifted vertically downwards by 4 units each to points
are shifted vertically downwards by 4 units each to points 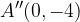 and
and 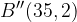 , respectively to produce the blue curve.
, respectively to produce the blue curve.
Hence, we can deduce that:
the radical function 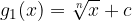 is produced by shifting each point of the basic radical function
is produced by shifting each point of the basic radical function 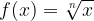 vertically upward by c units.
vertically upward by c units.
the radical function 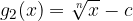 is produced by shifting each point of the basic radical function
is produced by shifting each point of the basic radical function 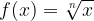 vertically downward by c units.
vertically downward by c units.
Here, the basic radical functions are transformed by adding a real number c to its radicand. We shall illustrate the forms by drawing their graphs on the same axes.
We tabulate the functions involved:
Now, we graph the functions.
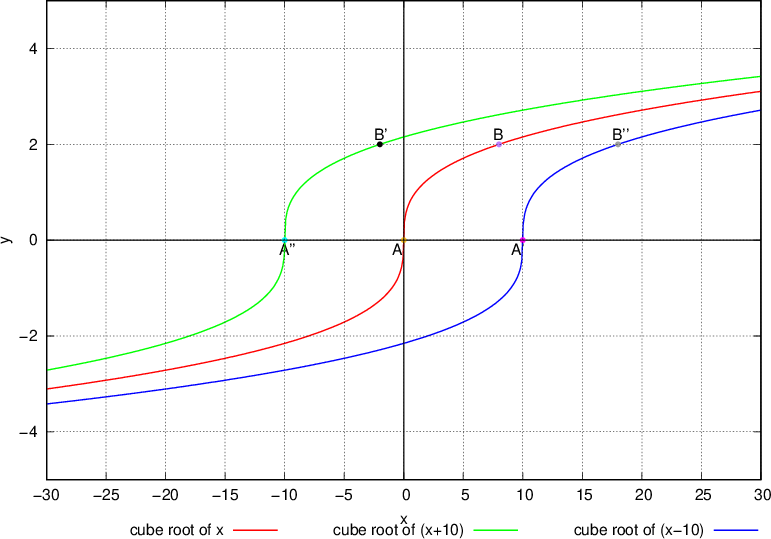
From the graph above, it can be seen that the red curve represent the basic radical function,  , the green and blue curves represent the transformed radical functions
, the green and blue curves represent the transformed radical functions 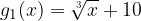 and
and 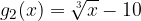 , respectively.
, respectively.
For example, points 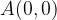 and
and 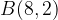 shifted horizontally left by 10 units each to points
shifted horizontally left by 10 units each to points 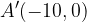 and
and 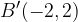 , respectively to produce the green curve. Furthermore, points
, respectively to produce the green curve. Furthermore, points 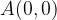 and
and 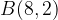 shifted horizontally right by 10 units each to points
shifted horizontally right by 10 units each to points  and
and 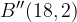 , respectively to produce the blue curve.
, respectively to produce the blue curve.
Hence, we can deduce that:
the radical function 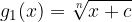 is produced by shifting each point of the basic radical function
is produced by shifting each point of the basic radical function 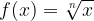 horizontally left by c units.
horizontally left by c units.
the radical function 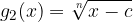 is produced by shifting each point of the basic radical function
is produced by shifting each point of the basic radical function 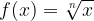 horizontally right by c units.
horizontally right by c units.
Here, the basic radical functions are transformed by multiplying it by a real number, A. We shall illustrate the forms by drawing their graphs on the same axes.
We tabulate the functions:

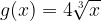

Now, we graph the function f, g and h for comparison.
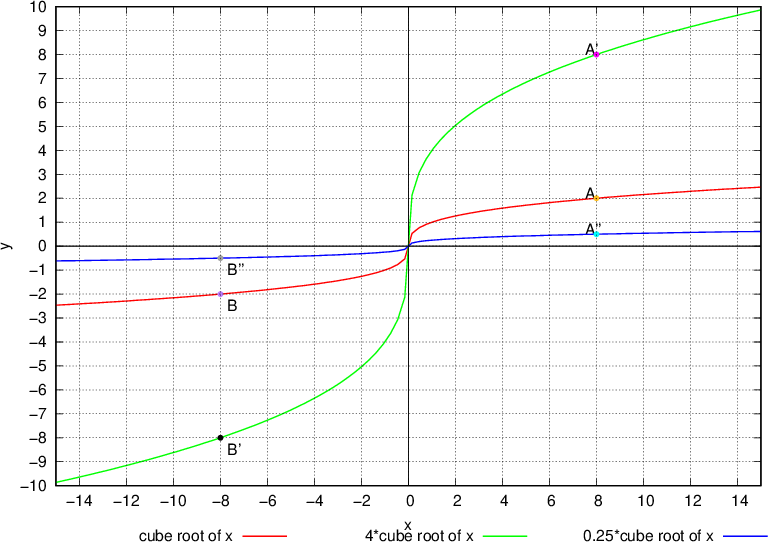
From the graph above, it can be seen that the red curve represent the basic radical function,  , the green and blue curves represent the transformed radical functions
, the green and blue curves represent the transformed radical functions 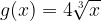 and
and  , respectively.
, respectively.
For example, points 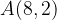 and
and 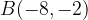 stretched vertically by a factor of 4 units each to points
stretched vertically by a factor of 4 units each to points  and
and 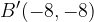 , respectively to produce the green curve.
, respectively to produce the green curve.
Furthermore, the same points 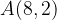 and
and 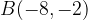 shrink vertically by a factor of 4 units each to points
shrink vertically by a factor of 4 units each to points 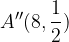 and
and 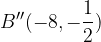 , respectively to produce the blue curve.
, respectively to produce the blue curve.
Hence, we can deduce that:
the radical function 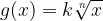 is produced by stretching (or enlarging) each point of the basic radical function
is produced by stretching (or enlarging) each point of the basic radical function 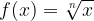 vertically by a factor of k units.
vertically by a factor of k units.
the radical function 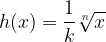 is produced by shrinking (or reducing) each point of the basic radical function
is produced by shrinking (or reducing) each point of the basic radical function 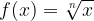 vertically by factor of k units.
vertically by factor of k units.
Here, the basic radical functions are transformed by multiplying it by the constant, -1. We shall illustrate the forms by drawing their graphs on the same axes.
We tabulate the function:


Now, we graph the function f and g for comparison.

From the graph of the cube root above, it can be seen that the red curve represents the basic radical function,  , the green curve represents the transformed radical function
, the green curve represents the transformed radical function 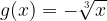 .
.
For example, each of the points 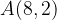 and
and 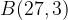 are flipped vertically or reflected across the x-axis to points
are flipped vertically or reflected across the x-axis to points 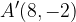 and
and 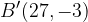 , respectively to produce the green curve.
, respectively to produce the green curve.
Hence, we can deduce that the radical function  is produced by flipping vertically or reflecting across the x-axis, each point of the basic radical function
is produced by flipping vertically or reflecting across the x-axis, each point of the basic radical function 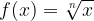 .
.
We shall plot the graph of  given that
given that 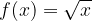 .
.
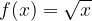
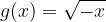
Now, we graph the function f and g for comparison.
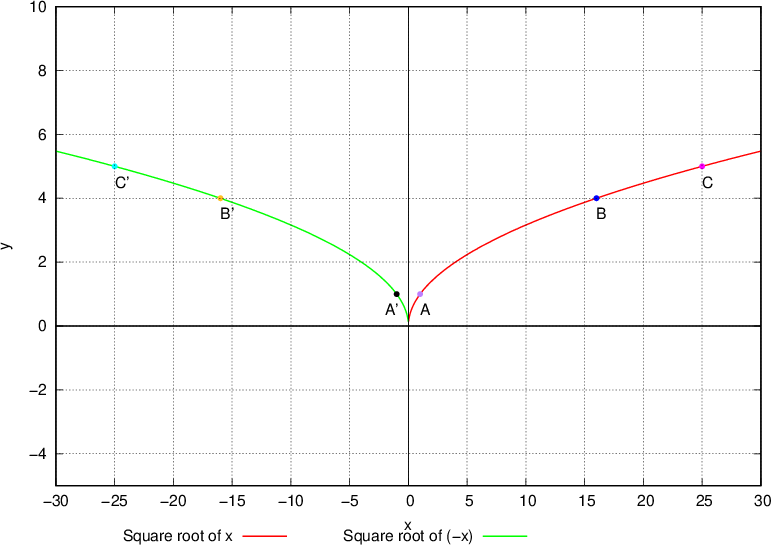
From the graph of the square root above, it can be seen that the red curve represents the basic radical function, 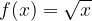 , the green curve represents the transformed radical function
, the green curve represents the transformed radical function 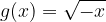 .
.
For example, each of the points 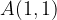 and
and 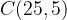 are flipped horizontally or reflected across the y-axis to points
are flipped horizontally or reflected across the y-axis to points 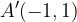 and
and  , respectively to produce the green curve.
, respectively to produce the green curve.
Hence, we can deduce that the radical function 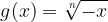 is produced by flipping horizontally or reflecting across the y-axis each point of the basic radical function
is produced by flipping horizontally or reflecting across the y-axis each point of the basic radical function 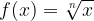 .
.
In conclusion, let's quickly consider situations in which two or more transformations are combined.
When drawing the graph of radical functions with combined transformations, we need to imply a correct order of transforming the basic function.
We shall take one more example for a better understanding.