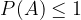Personal collections


In the chapter Probability of event we learned about the properties of probability, i.e. probability axioms and Kolgomov's axioms. In this chapter, we will learn about some new features and at the same time some that we already know. This time, we will also prove their claims.
The use of these proven statements can noticeably make it easier for us to calculate the probability of events and offer a faster way of solving exercises that we solved in a longer way before introducing the claims.
We know that an impossible event - I mark an event with the letter N - can never happen. It is therefore obvious that the probability of such an event is equal to 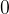 .
.
The probability of an impossible event N is equal to 0:

Proof
Let events A and N be incompatible. Then, taking into account the axiom of probability, we can write:
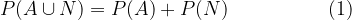
Since obviously event N cannot happen, we can also write at the same time:
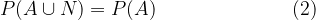
The obtained statements (1) and (2) are equated and we get:
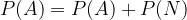
From which it clearly follows:

The probability of the event A of the opposite event A ' is equal to 1 - the probability of the event A.
The probability of the opposite event (A ') is obtained by subtracting the probability of the underlying event (A) from 1:

Proof
The definition of the opposite event A ' says that they are incompatible with the basic event A. Therefore, the following statements apply:
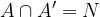
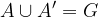
where N is an impossible event and G is a definite event. According to the axioms of probability we can therefore write:
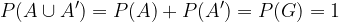
Which is really the same:

Or:

The probability of an event that is mode of some other event is always less than or equal to the probability of that other event.
If the event is A is contained in B; that is, 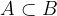 , then:
, then:
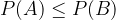
Proof
If 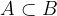 holds, then event B can be written as the sum of two incompatible events: A and B - A. Its probability is as follows:
holds, then event B can be written as the sum of two incompatible events: A and B - A. Its probability is as follows:

We simplify:
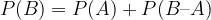
For any event, its probability is considered to be a non-negative number: 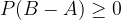 , so obviously the inequality must apply:
, so obviously the inequality must apply:
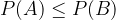
The probability of the difference of two arbitrary events A and B is equal to the difference of the probability of one of the events and the probability of the intersection of both events.
The probability of the difference of two arbitrary events A and B is written as:
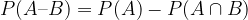
Proof
Event A is written as the sum of two incompatible events, event 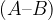 and
and 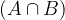 :
:

Using the axiom to calculate the probability of incompatible events, we obtain the following relation:
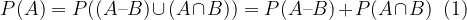
We rearrange the obtained statement (1) and get:
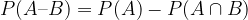
How do we calculate the probability of the sum of two arbitrary events when e.g. events are not incompatible?
The probability of the sum of two arbitrary events A and B is written as:
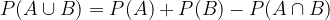
Proof
Let the events A and B be arbitrary. Events A - B and B are considered incompatible, and their sum is equal to the sum of events A and B: 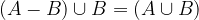 . Taking into account the axiom of probability of two incompatible events, we can write:
. Taking into account the axiom of probability of two incompatible events, we can write:

Taking into account the delay difference statement, the obtained probability 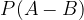 can be written with
can be written with 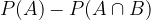 . We get:
. We get:
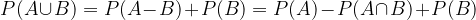
Let's rearrange and get:
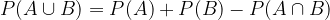
The probability value of any event can never be greater than 1.
The probability of any event can never exceed 1:
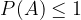
Proof
For each event, the mode of the finished event is: 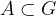 . At the same time, we know that the following is considered a definite event:
. At the same time, we know that the following is considered a definite event: 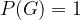 . Therefore, taking into account the axioms of probability and the above proven relationship between an event that is the mode of another event, we can conclude that:
. Therefore, taking into account the axioms of probability and the above proven relationship between an event that is the mode of another event, we can conclude that:
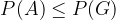
And: