Personal collections


In everyday conversations, we often express our assessment of the probability that an event will happen, for example: "I am one hundred percent sure that I will get a raise.", "It will definitely rain today.", " It's impossible for her not to succeed! "etc. In these sentences, we express our beliefs about the outcome of a random event. In this case, a random event is an event whose existence we cannot or do not know for sure to predict in advance: it can happen, but it can not.
With probability terms, we basically estimate whether a random event will happen or not. Depending on how often an event occurs, and how many attempts we have to make in doing so, we assign “his” probability to a given event. This probability, instead of estimating it subjectively, can be mathematically calculated much more concretely.
The probability of an event is a number that indicates the probability that an event will occur in one attempt, or whether an event will occur at all or not.
Probability is denoted by a capital letter P, and individual events are always named. Thus, the probability of an event named by the letter A is denoted by:
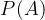
The probability of an impossible event N is always equal to 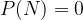 , and the probability of a certain event G is always equal to
, and the probability of a certain event G is always equal to  .
.
For the probability of any event A the following applies:
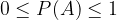
There are several mathematical methods for determining the probability of an event. We will get to know two, the statistical definition of probability and the classical definition of probability.
In the material Events in probability for KS4 we talked about events and experiments; let's repeat quickly: the experiment is e.g. with a coin. The event is the result of an experiment, in the case of a coin we have two possible events: the head or the tail falls. The events are equivalent, as there is an equal chance of the head falling or the tail falling.
The experiment can be repeated several times, counting the number of times the selected event occurred, which should be named as an event A (eg the coat of arms falls). Relationship between:
the number of attempts in which the event occurred A and
the number of all iterations of the experiment
we call the relative frequency of event A. The relative frequency of an event is the number assigned to a given experiment.
The relative frequency of the event is the ratio between the number of realizations of the event A (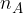 ) and the number of all attempts
) and the number of all attempts 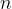 :
:
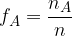
Let's look again at the example above and write down some remarks:
although we toss a fair coin, where in theory the probability (or relative frequency of the event) for head or tail is the same, i.e. 0.5, with a finite number of attempts we almost never get the exact value 0.5;
the greater the number of attempts, the closer the obtained relative frequency of the event (say event A) approaches the theoretical value, i.e. 0.5, the probability of the event.
Both findings actually suggest the law of statistics, which states that as the number of repetitions of an experiment increases, the relative frequency of the event begins to approach a certain number, the statistical probability of the event A.
The statistical or experimental probability of the event A is the number to which the relative frequency of the event A approaches with increasing repetitions of the experiment and stabilizes at this number.
We can say that the statistical probability of an event A is a number at which - with a sufficiently large number of attempts - the ratio between the 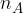 number of realizations of event A and the
number of realizations of event A and the 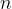 number of performed experiments stabilizes.
number of performed experiments stabilizes.
Calculating the probability of an event in such an empirical way (with experiments) is cumbersome, it usually takes a lot of time, often even longer than a human life. Therefore, in the search for a way to calculate the probability of an event without conducting experiments, the French mathematician Laplace determined a theoretical formula of probability, which today we call the classical definition of probability.
The classical or theoretical definition of probability says: if all elemental events of a sample space are equally probable (equivalent), and event A is an event composed of possible outcomes of events from this sample space, the probability of event A is equal to:

where m is the number of favorable outcome of events for A and n is the number of all elementary outcomes of the experiment.
Like the statistical definition of probability, the classical definition of probability applies only in the sample space of the experiment, where all its outcomes events are equal to each other and thus equally probable. Such a sample space is called a symmetric sample space.
Both definitions of the probability of events in a symmetric sample space, both the statistical and the classical definition, have in common the following properties, which are called probability axioms.
Probability axioms:
The probability of random event A is a non-negative number:

The probability of a definite event G is equal to 1:

Probability of the sum of incompatible events A and B; if  applies, it is equal to the sum of the probabilities of individual events:
applies, it is equal to the sum of the probabilities of individual events:
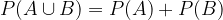
How do we calculate the sum of two compatible events A and B; so when their cross section is not zero, we will look in the next chapter.
The probability of an impossible event N is equal to 0:
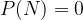
The probability of an event A of the opposite event A ' is equal to 1 - the probability of the event A:
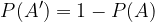
This chapter is intended for more demanding readers. The chapter can be omitted by the reader without compromising the understanding of the entire chapter.
As already mentioned, the classical definition of probability applies only in the symmetric sample space of the experiment, where all its elementary events are equally probable.
By considering the axioms of probability and the properties of the sample space, we derive the probability of the event in the symmetric sample space.
Let them be:
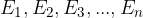
elementary events of an experiment. Obviously, their sum is considered a definite event:

Since the elementary events of the pair are considered incompatible, they can be written with the axiom of probability (3):
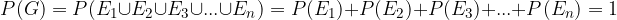
Since all elementary events of a symmetric sample space are equal, the following applies:
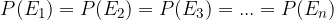
It follows that:
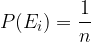
So if an event A is considered to have m favorable outcome, then its probability is really the same:
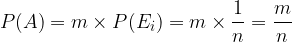
We can calculate the probability of an event in a symmetric sample space. But sometimes the symmetry of the sample space of an experiment is difficult to ensure, from which it follows that the classical definition of the probability of an event is very limited. As a typical example of a constraint, we can take the calculation of the probability of an event when throwing a fraudulent dice: since the probabilities of obtaining the selected number of points differ from each other, it is obviously no longer a symmetric sample space.
Therefore, to calculate the probabilities of events from asymmetric sample spaces — those where elementary events can have different probabilities we consider the axiomatic definition of probability of the Russian mathematician, who defines the probability of an event as a function of the sample space.
The axiomatic definition of probability defines probability as a mapping that assigns a real number to each event from the set of all events of an experiment if it satisfies the rules of Kolgomorov's three axioms.
Kolgomorov's axioms are properties that apply to all definitions of probability (classical, statistical, axiomatic ...), and say:
Function is positive:

Function is standardized:

If  applies, then:
applies, then:
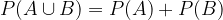
Since these properties apply to arbitrary definitions of probability, the given axioms also apply to the calculation of the probability of events when the sample space is not symmetric. In this case, the probabilities of elementary events are considered to be different.
The calculation of the probability of an event from an asymmetric sample space 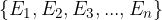 is possible only if the individual probabilities of elementary events
is possible only if the individual probabilities of elementary events  are known. As with the probabilities of events from a symmetric sample space, the probabilities of these elementary events must be subject to:
are known. As with the probabilities of events from a symmetric sample space, the probabilities of these elementary events must be subject to: