A basketball team consists of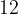 
players: 
defenders,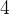 
wingers and 
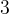centres. One of the defenders is named Samuel and one of the centers is Jack. The remaining players have different names.
How many ways can all players line up if Samuel has to stand in line first and if the centers have to stand together (there are no other restrictions)?
How many ways can a coach put together a top five if it needs to have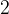 
defenders, 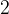wingers and 
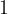center?
In training, the coach will classify players randomly into three groups of 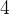players each: the first group will practice free throws, the second group a game in defense, the third group a game in attack.
Calculate the probability of events:
Samuel and Jack will practice the game in defense,
Samuel will practice free throws, and Jack will play in attack
.
