Personal collections


In the following, we will look at the proportion and percentage change separately:
We encounter proportions in everyday life (e.g., squeezing juices, building a house, travel and speed e.t.c.). In the case of problems arising from proportions, there are usually two quantities that are in a simple relationship with each other. This relationship can be:
Directly proportional
Inversely proportional
Let’s look at both relationships in more detail.
Two quantities are directly proportional to each other if:
one quantity increases or decreases by certain times while at the same time the second quantity increases or decreases by exact same times.
Two quantities are inversely proportional to each other if:
one quantity increases by certain times while at the same time the second quantity decreases by exact same times or vice versa.
We also encounter a changes in bills in our everyday life (price increases, price reductions, e.t.c.). Most often we are always interested in what the relative change is.
Relative change is a measure of how much a quantity has changed in relative to its original value and it is calculated as:
Relative change can also be written as percentages.
The result of the relative change can be expressed as a fraction and also in percentages. In other words, percentage change is the representation of a relative change as a percentage.
The easiest way to do this is by using the formula:
Percentage Change:
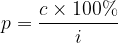
where c represents the change, i the initial amount.
If we denote the amount of percentages by p, then in we can say:
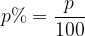
Let's use the above formula in the following example below:
There is a link between the percentage change and the relative change.
Let’s obtain the relationship between the two using the formula for relative change :