where the coefficients a, b and c are any real numbers. The coefficient a is called the coefficient of the quadratic term or the leading coefficient, b the coefficient of the linear term and c the constant term.

The coefficient a cannot be equal to 0, because then the equation is no longer quadratic.

Regarding quadratic equations, it should be emphasized at the outset that, unlike linear equations, where we write a constant term on the right, we arrange them consistently so that the right side is equal to 0, and on the left we classify the terms by decreasing powers.

Simplifying quadratic equations

Example of simplifying a quadratic equation

We have given the equation:

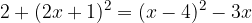
We simplify the equation:

	We square the binomial:
	We move the terms to the left and simultaneously arrange them in descending powers:
	We add the same kind of terms:

Hence, we got the quadratic equation in general form, where:

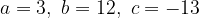
Generalisation of simplifying quadratic equation

Given the equation:

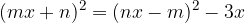
Simplify the equation.

Let's simplify the equation:

	We obtain the square of the binomials:
	We move the terms to the left and at the same time arrange them in descending powers:
	We collect like terms:
	We factorise where we have common terms:
	We obtain the quadratic equation in general form, where:

Solving quadratic equations

The quadratic equation has two solutions, which are calculated according to the form:

where D is the discriminant calculated by the form:

For the solution of a quadratic equation we have as many as six different expressions for it: solutions of the quadratic equation or zeros of the quadratic equation or roots of the quadratic equation or zeros of the quadratic function or intersection of the quadratic function with the x-axis or intersection of the quadratic function with the abscissa.

The nature of the solutions of the quadratic equation depends on the discriminant D:

if 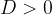, the equation has two different real solutions.
if 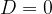, the equation has only one repeated real solution.
if is 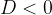, the equation has no real solution.

The equation has two complex solutions (conjugate complex numbers), which we will discuss in the chapter Complex numbers.

Some cases in solving quadratic equations:

Case D> 0

We have a quadratic equation:

The coefficients of the quadratic equation are: a = 1, b = -2 and c = -11. Solve the quadratic equation by first calculating the discriminant according to the form:

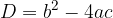
Let's obtain the discriminant:

	We insert the values of the coefficients of the quadratic equation into the form:
	We calculate:

The discriminant value is 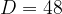. Since the discriminant is greater than 0, we know that the quadratic equation has two different real solutions. We calculate them using the form:

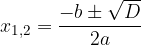
Let's obtain the roots of the equation:

	We insert the values of the discriminant and the coefficients of the quadratic equation into the formula:
	The value below the root is written in the form of a product to simplify using surds:
	We simplify the surd:
	We simplify:
	We simplify:

The solutions of the quadratic equation are:

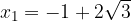and

Case D = 0

We have a quadratic equation:

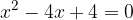
The coefficients of the quadratic equation are: a = 1, b = -4 and c = 4. Solve the quadratic equation by first calculating the discriminant according to the form:

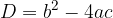
Obtaining the discriminant:

	We insert the values of the coefficients of the quadratic equation into the form:
	We calculate:

The discriminant value is 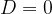. Since the discriminant is equal to 0, we know that the quadratic equation has only one double real solution. It is calculated using the form:

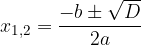
Let's obtain the roots of the equation:

	We insert the values of the discriminant and the coefficients of the quadratic equation into the formula:
	We express the radicand as a product so as to simplify using surds:
	We separate the expression and simplify:

The solutions of the quadratic equation are: .

Case D < 0

We have a quadratic equation

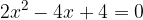
The coefficients of the quadratic equation are: a = 2, b = -4 and c = 4. Solve the quadratic equation by first calculating the discriminant according to the form: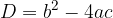

Let's obtain the discriminant:

	We insert the values of the coefficients of the quadratic equation into the form:
	We calculate:

The discriminant value is 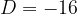. Because the discriminant is negative, the equation has no realistic solutions. The equation has two complex solutions (conjugate complex numbers), which we will learn to calculate in the chapter Complex numbers.

Solving special forms of quadratic equations by factorisation

In the previous chapter, we learned that with the help of two forms:

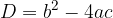
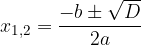
we can solve any quadratic equation. Solutions or roots of some special forms of quadratic equations can also be obtained by simpler and faster procedures with the help of factorisation, so let's take a look at them:

Case b = 0 (generalisation)

In the case where the linear term b = 0, the general form of the quadratic equation is transformed into:

The solution is derived by first converting the quadratic equation into a zero or factorized form. In a set of real numbers, the equation can be written in zero form only if a and c have opposite signs. How to write an equation in zero form if a and c have the same sign is discussed in the chapter Complex numbers.

Let's obtain thefactorised form:

	Let us point out the coefficient a:
	We transform the expression into the difference of squares.
	Disassemble the expression. In a set of real numbers, the expression can be decomposed only if a and c have opposite signs. How the expression is decomposed if a and c have the same sign and we get a negative value below the root is discussed in the chapter Complex numbers.
	We divide the equation by a:
	We obtained the quadratic equation in the so-called zero or factorized form. The product of two factors is equal to 0 when the first or second factor is equal to 0. Considering this fact, the equation decomposes into two linear equations:

Solve the first (linear) equation:

	Let's take the constant term to the right:
	We get the first solution:

Solve the second (linear) equation:

	Let's take the constant term to the right.
	We get another solution

Case b = 0 (practical example)

We have the equation:

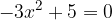
The solution is derived by first converting the quadratic equation into a zero or factorized form:

Let's write the equation in a factorized form:

	We multiply the equation by (-1):
	We factor out 3:
	Let's factorise using the difference of squares:
	We divide the equation by 3.
	We obtained the quadratic equation in the so-called zero or factorized form: The product of two factors is equal to 0 when the first or second factor is equal to 0. Considering this fact, the equation decomposes into two linear equations:

Solve the first (linear) equation:

	We get the first solution:

Solve the second (linear) equation:

	We get another solution:

Case c = 0 (generalisation)

In the case when the constant term c = 0, the general form of the quadratic equation is transformed into:

The solution is derived by first converting the quadratic equation into a zero or factorized form:

Let's write the equation in a factorized form:

	We factor out x:
	We obtained the quadratic equation in the so-called zero or factorized form: The product of two factors is equal to 0 when the first or second factor is equal to 0. Considering this fact, the equation decomposes into two linear equations:

The first equation has already been solved, so we solve the second (linear) equation:


	We divide by a:

Case c = 0 (example)

Let's have the equation:

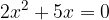
The solution is derived by first converting the quadratic equation into a zero or factorized form.

Let's write the equation in a factorized form:

	We factor out x:
	We obtained the quadratic equation in the so-called zero or factorized form. The product of two factors is equal to 0 when the first or second factor is equal to 0. Considering this fact, the equation decomposes into two linear equations:

The first equation has already been solved, so we solve the second (linear) equation:


	We divide by 2.
	We get another solution.

Case a = 1 (generalisation)

In the case where the leading term is a = 1, the general form of the quadratic equation is transformed into:

The quadratic trinomial of the form 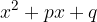is first disassembled on the basis of the same equation, by means of which it is converted into a zero or factorized form:

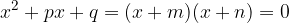
Factorisation is possible only if q can be written as the product of two factors m and n whose sum is equal to p.

Solve the factorised equation:

	We obtained the quadratic equation in the so-called zero or factorized form. The product of two factors is equal to 0 when the first or second factor is equal to 0. Considering this fact, the equation is splitted into two linear equations:

Solve the first (linear) equation:

	We get the first solution:

Solve the second (linear) equation:


	We get another solution:

Case a = 1 (example)

We have given the equation:

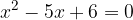
The coefficients are a = 1, p = - 5 and q = 6.

Let's factorise the expression on left hand side:

	Since we know that the coefficient q = 6 is the product of two factors m and n, we perform experiments with integers in mind. The number 6 can be written as a product of integers in four ways:
a) b) c) d)	The numbers - 2 and - 3 under b) form the sum of - 5, as much as p. The numbers sought m and n are therefore: - 2 and - 3:

Factorise the given equation according to the form and solve:

	We obtained the quadratic equation in the so-called zero or factorised form: The product of two factors is equal to 0 when the first or second factor is equal to 0. Considering this fact, the equation decomposes into two linear equations:

Solve the first (linear) equation:

	We take the constant term to the right:
	We get the first solution

Solve the second (linear) equation:

	We take the constant term to the right:
	and we get another solution

Zero form of the quadratic equation

The general form of the quadratic equation: in zero form using the notation:

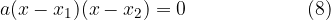
where are:

a square term coefficient or leading coefficient and
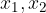solutions of the quadratic equation, which are calculated according to the form:

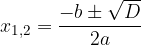
where D is the discriminant calculated by the form:

We have two different terms for the zero form: zero form or factorized form. The process is called factorization.

All quadratic equations can be written in zero form using the form for calculating the solutions of the quadratic equation (also the special forms of quadratic equations from the previous chapter).

material editor: Amarachi Akobundu