A quadratic function is a real function with a regulation in the so-called general form:
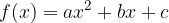
where the coefficients a, b and c are any real numbers. The coefficient a is called the coefficient of the quadratic term or the leading coefficient, b the coefficient of the linear term and c the constant, free, free, or constant term.
The coefficient a cannot be equal to 0, because then the function is no longer quadratic.
The graph of a quadratic function is called a parabola. The shape of the parabola is determined by the leading coefficient a:
If the leading coefficient is a> 0, the parabola is turned upwards and has the form:
If the leading coefficient is a <0, the parabola is turned downwards and has the form:
The width of the parabola depends on the absolute value of the leading coefficient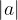 
. The higher the absolute value, the narrower and steeper the parabola:
Write the general form of the quadratic function 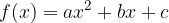in zero form using the notation:
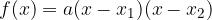
where are:
a square term coefficient or leading coefficient and
zero quadratic function.
The zeros of the quadratic function are calculated by the form:
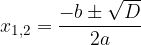
where D is the discriminant calculated by the form:
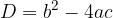
Zero functions are those numbers x for which the value of the function f (x) is equal to 0. Zeros tell us where the function intersects the x axis. In this case, the number and character of zeros of the quadratic function depends on the discriminant D.
Let's see how the zeros of a quadratic function depend on the discriminant D:
If D> 0, the parabola has two different real zeros 
the parabola intersects the x-axis, ie it can have one of the following forms:
for a> 0
for a <0
If D = 0, the parabola has a single double real zero 
the parabola touches the x-axis, ie it can have one of the following forms:
for a> 0
for a <0
If D <0, the parabola has no zeros 
the parabola does not intersect and does not touch the x-axis, ie it can have one of the following forms:
for a> 0
for a <0
The general form of the quadratic function: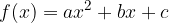 
is written in vertex form with the help of the notation:
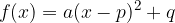
where are:
a square term coefficient or leading coefficient and
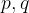coordinates of the vertex of the parabola T (p, q).
The coordinates of the vertex are calculated by the equations:
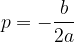
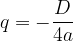
where D is the discriminant calculated by the form:
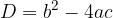
Curve themes T (p, q) is the point in plane geometry where the curvature of the curve reaches an extreme (minimum or maximum) value.
Let's look at the geometric meaning of the vertex:
If a> 0 the parabola is turned upwards, then it has in the vertex T (p, q) at p the smallest value q:
If a <0 the parabola is turned downwards, then it has in the vertex T (p, q) at p the largest value q:
From the above graphs we understand that the symmetric axis of the parabola is parallel to the ordinate axis and its equation is:
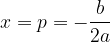
The vertex shape of a square function can also be obtained by completing the general shape to a perfect square.
Derive the vertex form of the quadratic function by completing to the perfect square:
We obtained the vertex shape of the quadratic function.
When drawing the parabola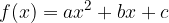 
, which is given in general form, we use the key points, which are:
zero square function
There are zero points where the function intersects or touches the x axis and is subject to y = 0:
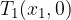
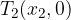
initial value of the function
The initial value of a function is the point at which the function intersects the y axis and is subject to x = 0:
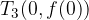
function topics
The topic is the point where the quadratic function has an extreme (minimum or maximum) value:
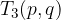
initial value mirror image
Since the quadratic function is symmetric with respect to the vertical through the themes, we can use a point as an additional reference point, which is a mirror image of the initial value:
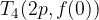
Draw the calculated key points into the coordinate system and draw a graph of the given quadratic function through them. The forms for calculating key points are:
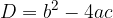
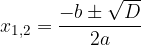
From the function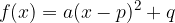 
, which is given in vertex form, we understand the following data, important for drawing its graph:
initial function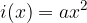 
and
topics T (p, q).
First we draw the initial function 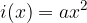, which is the simplest form of a quadratic function (because b = 0 and c = 0) and can therefore be drawn using tabulation. For x - e we choose arbitrary values (usually 
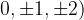and calculate the corresponding functional values. This gives the points through which the function passes.
Draw the obtained points into the coordinate system and draw the initial function 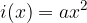through them.
The function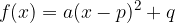 
is then drawn by moving the drawn starting graph 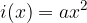rigidly so that its theme is at the point T (p, q), which is the theme of the given function.
The mutual position between the parabola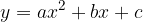 
and the line 
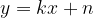is determined by solving the system of their equations:
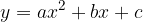
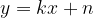
Solve it by switching mode. In the first equation, replace the unknown y with the expression in the second equation:
The abscissa of the intersection of the parabola and the line is the solution of the quadratic equation:
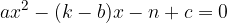
which has coefficients:
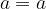
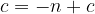
The mutual position of the parabola and the line depends on the discriminant D, which is calculated according to the form:
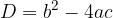
The discriminant affects the position between the quadratic function and the equation as follows:
If D> 0, the line intersects the parabola at two points
If D = 0, the line touches the parabola, that is, its tangent
If D <0, line and parabola have no common point
