Personal collections


A quadrilateral is a geometric figure with four vertices and four sides.
Since we are considering simple figures, we limit ourselves to quadrilaterals whose sides meet only at the vertices and do not intersect with each other. We call them simple quadrilaterals.
Simple quadrilaterals are divided into:
Convex quadrilaterals
For convex quadrilaterals:
Each interior angle is less than or equal to 180°.
Each angle between any two vertices is located inside or on the edge of the figure.
Concave quadrilaterals
For concave quadrilaterals:
One interior angle is greater than 180°.
There is an angle between two vertices, part of which is located outside the figure.
You can read more about convex and concave polygons in the chapter on polygon.
In this chapter, we will focus mainly on convex quadrilaterals. Special consideration will be given to:
Parallelogram (this also include rhombus, rectangle, square),
Trapezium
Kite
Other quadrilaterals:
Cyclic quadrilateral
Tangential quadrilateral and
Bicentric quadrilateral
Parallelogram
A parallelogram is a quadrilateral with two pairs of parallel sides. The pair represent the opposite side:
The following applies to the sides and interior angles of a parallelogram:
The parallel sides are equal in length.
Opposite angles are equal.
Adjacent angles are supplementary.
Taking into account the above properties, the sketch of a parallelogram:
Diagonal
A diagonal is a line that connects non-adjacent vertices of a parallelogram.
A parallelogram has two diagonals that bisect each other. Let them be marked with e and f:
A parallelogram is a symmetric figure with the center of symmetry at the intersection of the diagonals.
Height
The height of a parallelogram is the perpendicular distance between the parallel sides.
The parallelogram has two heights. We denote them by 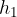 and
and 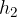 :
:
Interior angle
The interior angle is form from the intersection of the sides. The interior angles are marked such that the angles at vertices A and C are denoted by 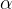 , and angles at vertices B and D by
, and angles at vertices B and D by 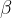 :
:
The sum of the interior angles of a parallelogram is 360°.
Exterior angle
The exterior angle is supplementary to the corresponding interior angle. We mark the exterior angles with their corresponding interior angle but with an apostrophe:
The sum of the exterior angles of a parallelogram is 360°.
Rhombus
Compared to a parallelogram, a rhombus has all its sides equal.
Properties of Rhombus:
All sides are equal in length.
Opposite angles are equal.
Adjacent angles are supplementary.
The diagonals intersect at right angles.
Taking into account the above characteristics, the sketch of a rhombus is as follows:
Rectangle
Compared to parallelogram, all angles of a rectangle are equal.
Properties of Rectangle:
The parallel sides are equal in length.
All angles are equal and measure 90°.
The diagonals are equal and bisect at the center.
Taking into account the above properties, the sketch of a rectangle is as follows:
Square
The square has all sides and all angles in comparison with parallelogram equal.
Properties of Square:
All sides are equal in length.
All angles are equal and measure 90°.
The diagonals are congruent, bisecting and intersecting at right angles.
Taking into account the above properties, the sketch of a square is as follows:
A square is a regular quadrilateral because all its length and angles are equal.
The perimeter of a parallelogram is calculated as follows:
General formula for the perimeter of a parallelogram:
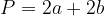
The Perimeter for types of parallelograms are:
Perimeter for Rhombus and Square:

Perimeter for Rectangle:
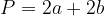
The area of a parallelogram is calculated as follows:
General formula for area of a parallelogram:
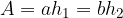
The area for types of parallelograms are:
area of Rhombus:
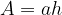
Area of Rectangle:
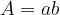
Area of Square:

When a parallelogram is divided into triangles, we can use triangular theorems.
Trapezium
A trapezium is a quadrilateral with one pair of parallel sides.
The pair represents the opposite side; these two sides are called bases, and the remaining two sides are called slant sides:
In trapezium, there are adjacent interior angles along the slant sides which are supplementary:
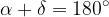
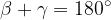
Diagonal
A diagonal is a line that connects non-adjacent vertices of a trapezium.
The trapezium has two diagonals:
For the diagonals of a trapezium, the ratio between the diagonal division sections is considered to be equal to the ratio between the lengths of the bases:
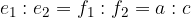
where the first is the diagonal
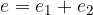
and the second diagonal

Midline
The midline is a line that is parallel to the bases and connects the centers of the non-parallel sides b and d.
The length of the midline is equal to the average of the bases a and c:
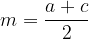
Height
The height of trapezium is the perpendicular distance between the bases.
Let it be denoted with h:
Interior angle
The interior angles may be obtuse or acute angles formed from the intersection of the sides. The interior angles are marked with 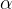 ,
, 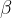 ,
, 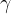 and
and  :
:
The sum of the interior angles of a trapezium is 360°.
Exterior angle
The exterior angle is supplementary to the corresponding interior angle. We mark the corresponding exterior angle similar to the interior angles but with apostrophe:
The sum of the external angles of the trapezium is 360°.
Isosceles trapezium
Compared to the general trapezium, the isosceles trapezium has equal length of slant sides and adjacent internal anglesalong the bases.
Properties of an isosceles trapezium:
The slant sides of the trapezium are equal in length.
Adjacent interior angles along the bases are equal.
The diagonals are equal.
Taking into account the above properties, the sketch of an isosceles trapezium is as follows:
Rectangular trapezium
In rectangular trapezium, compared to the general trapezium, one of the non-parallel side is rectangular in shape.
Properties of a rectangular trapezium:
One of the sides is perpendicular to the base.
One of it's side is equal to the height of the trapezium.
Taking into account the above characteristics, the sketch of a rectangular trapezium is as follows:
The perimeter of trapezium is calculated as follows:
General formula for the perimeter of trapezium:
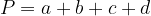
The perimeter for special types of trapezium is:
The perimeter of an isosceles trapezium:
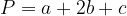
Perimeter of a rectangular trapezium:
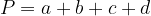
The area of trapezium is calculated as follows:
The general formula for area of trapezium is:

where m is the midpoint of the trapezium defined as:
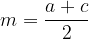
The area for special types of trapeziums are:
Area of isosceles trapezium:

With Pythagoras' theorem we express the height:
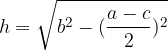
The area of an isosceles trapezium can also be written as:
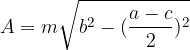
Area of rectangular trapezium:

since the height is equal to side d.
When we divide a trapezium into triangles, we can use triangle theorems.
Kite
A kite is a quadrilateral with two pairs of sides of equal length:
The following applies to the sides and interior angles of kite:
The kite has two pairs of adjacent congruent sides.
The angles between the unequal sides are equal and opposite.
Taking into account the above properties, the sketch of kite is:
Diagonal
The diagonal is the line connecting the non-adjacent vertices of the kite.
The kite is a symmetric geometric figure, with the bisector representing one of the diagonals.
The kite has two diagonals that intersect at a right angle. One of the diagonals represents the symmetry line of the figure and at the same time bisects the other diagonal:
Interior angle
The interior angle is a pair of an acute angles and an obtuse angle with sides running through the adjacent vertices. The angles at vertices A and C are denoted by 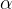 , and the angles at vertices B and D by
, and the angles at vertices B and D by 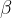 and
and  , respectively:
, respectively:
The sum of the interior angles of a kite is 360°.
Exterior angle
The exterior angle is supplementary to the corresponding interior angle. The exterior angles are convex. We mark the exterior angles similar as the interior angles but with an apostrophe:
The sum of the exterior angles of a kite is 360°.
The perimeter of a kite is calculated as follows:
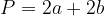
The area of kite is calculated as follows:
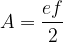
When we divide a kite into triangles, we can use triangle theorems.
Other quadrilaterals
Cyclic Quadrilateral
We can draw a circle to touch the vertices of a quadrilateral:
The cyclic quadrilateral has opposite angles which are supplementary:

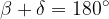
Tangential quadrilateral
We can draw a circle to touch all the sides of the quadrilateral in a tangential quadrilateral:
In a tangential quadrilateral, the sum of the lengths of the two opposite sides is equal to the sum of the lengths of the other two opposite sides:

Bicentric quadrilateral
If both cyclic and tangential quadrilateral are possible with a quadrilateral, then we have a bicentric quadrilateral. It is also called the chord tangent quadrilateral.
A circle can be inscribed as well as circumscribed in a bicentric quadrilateral:
The following laws apply in a bicentric quadrilateral:


