Light is electromagnetic waves, the same as, for example, radio waves. The properties of light include the following:
it is determined by the luminous flux or luminous power P[W].
the speed of light waves 
in airless space is given as:
If light penetrates a substance (glass, water, etc.), its speed decreases.
the frequency and wavelength of light waves are related by the formula:
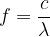
The frequency or wavelength determines the colour of visible light. Light with a longer or shorter wavelength than visible light is called infrared light and ultraviolet light:
Figure 1: Colours of visible light
A light source can emit light of a single wavelength (called monochromatic light). An example of monochromatic light is laser light. A source can also emit several wavelengths at the same time (we say that it emits a light spectrum). An example is the Sun, which radiates all wavelengths of visible light (the full spectrum).
The light source can be a point lamp that emits light in all directions equally, or it can be a lamp that emits light only in a certain direction (e.g. a reflector with a reflecting spherical or parabolic mirror that directs the rays in only one direction).
Similar to waves on a liquid, light propagates in the direction of wave rays, which are called light rays. If the light source is very small (point light), the light spreads from the light source radially in all directions. However, if the rays are parallel, they form a light beam. A light beam is therefore made up of light rays.
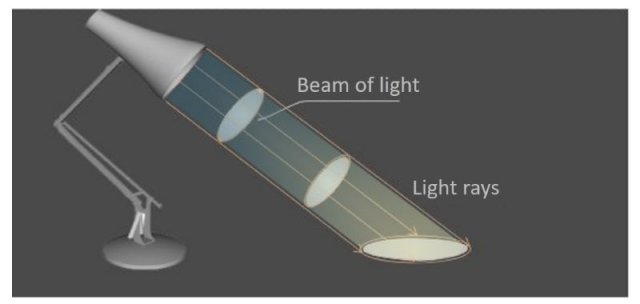
Figure 2: Light rays (arrows) and the light beam of a luminaire (in this case an elliptical figure) with directional light
As we said in the introduction, the speed of light changes when travelling in different substances. Let's consider light passing at a certain angle from a substance where it has a higher speed to a substance where it has a lower speed. We also say that the beam passes from an optically less dense medium (where the speed of light is higher) to an optically denser medium (where the speed of light is lower). Figure 3 shows the crests of the wave, which we also encountered in Water waves. Now let's call them light wavefronts. The distance between two wavefronts is the wavelength (see Figure 3).
Several light phenomena can be observed. The light is partly reflected and partly penetrates another substance, but at the same time its wavelength is reduced and it is refracted at the boundary surface:
Figure 3: Transition of light from an optically less dense to an optically denser medium
Part of the light is reflected at the boundary surface. The law of reflection applies. This says that when light hits a smooth surface, the angle of incidence 
is equal to the angle of reflection. The angle of incidence is the angle between the normal (vertical) and the incident ray, the same as the angle of reflection (see the angle in Figure 3).
In the case of light reflection, we always assume that the roughness of the boundary surface is much smaller than the wavelength. Otherwise, the reflected beam is scattered.
When light is reflected on a smooth surface, the light is reflected so that the angle of incidence is equal to the angle of reflection.
When passing from an optically less dense medium to an optically denser medium, the wavefronts are compressed. Since the distance between two wavefronts is equal to the wavelength, it means that the wavelength has decreased. Why?
We answer this using the fact that the frequencies in both mediums (substances) are equal. Therefore, we have:
If light passes from an optically less dense substance (medium) to an optically denser substance or vice versa, the wavelength changes. The wavelengths in both substances are in the same ratio as the speed of light in both substances:
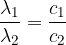
Light also refracts. This means that the angle of incidence is not the same as the angle of refraction. The wave chooses the path for which it spends the least time. This is Fermat's principle. The derivation of this law is quite demanding, so we will derive the law of refraction in a simpler way.
Let's take the case when light is incident at a certain angle into a substance, where its speed is reduced relative to the speed of the incident ray.
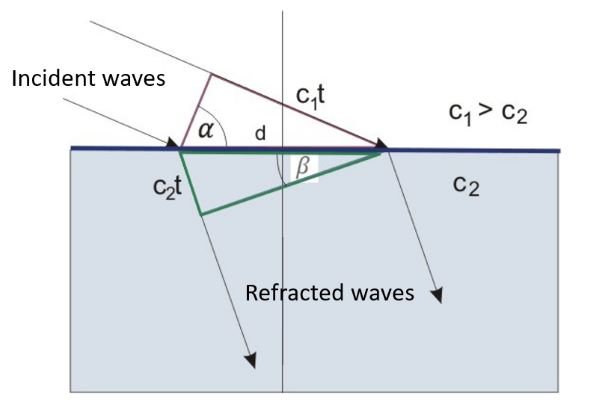
Figure 4: Refraction of light; here, let's pay attention to the angles and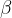 
, which, although indicated a little differently, are still the angles that determine the deflection of the beam from the normal to the boundary surface
The incident wave is incident at an angle to the normal on the boundary surface of two substances. In the first substance, the wave speed is 
, and in the second, 
(see Figure 4).
We note that:
On the contact surface, the wave travels a longer distance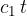 
in time 
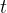(because the speed is higher) than on the other surface where it travels the distance 
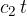in the same time 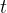. In Figure 4, two right triangles are marked on the upper and lower half of the boundary surface.
Let's take a look at the purple-bordered triangle above, from which we have:
And from the lower green-bordered triangle, we have:
From the two results for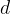 
above, we can say that:
If the above substance in Figure 4 is air or vacuum, we can write:
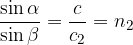
In this case,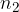 
is the refractive index of the other substance.
The refractive index tells us how much faster light travels in an airless space than in an observed substance.
We now reexpress equation (1). For this purpose, we multiply the numerator and denominator of the right side of the equation by :
Equations (1) and (2) are two forms of the law of refraction.
A ray falling obliquely on the boundary surface is partly reflected and partly penetrates the material. The part of the ray that is reflected is reflected at the same angle, with respect to the vertical, at which it was incident.
The part of the beam that penetrates the substance, however, penetrates at such an angle 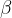that:
where is the angle at which the ray is incident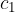, and 
and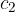 
are the velocities of light waves in the first and second substances.
The refractive indices for the first and second substances are:
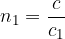
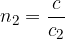
The law of refraction can also be written in the form:
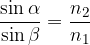
From the law of refraction, we can determine that if the ray passes into an optically denser substance (where the velocity is lower), it refracts towards the normal (vertical), and if it passes into an optically less dense substance (where the velocity is higher), it refracts away from the vertical (normal). Let's look at the refractive indices for some substances:
Let's assume that light passes from a substance with a lower speed of propagation to a substance with a higher speed of propagation, e.g. from water to air. Figure 4 also applies in this case, except that we reverse the direction of the beam:
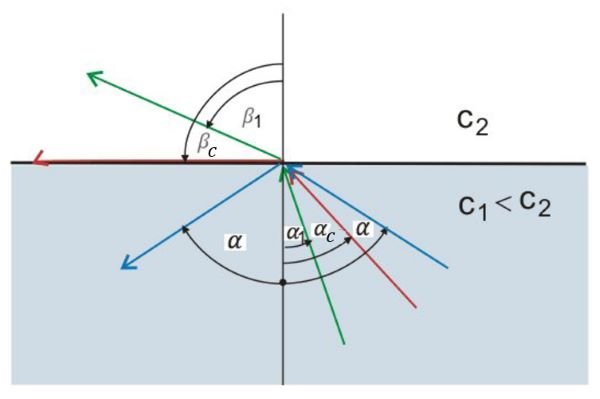
Figure 5: Refraction into an optically less dense medium (green ray), critical angle (red ray), and total internal reflection (blue ray)
The angle of refraction is now greater than the angle of incidence (green ray in Figure 5). Let's increase the angle of incidence so that the angle of refraction becomes exactly 90 degrees. We obtained the limiting angle of total reflection, this is called the critical angle. (see the red-coloured beam in Figure 5).
Let's find the critical angle 
:
We obtained the sine of the critical angle (Figure 5, red ray). If we further increase the angle of incidence (beyond the critical angle), the light beam is reflected at the boundary surface and no longer passes into the optically less dense substance (see the blue beam in Figure 5), this is called the total internal reflection. Then the law of reflection applies: the angle of incidence and that of the reflection are the same.
Total internal reflection occurs if a beam propagates from an optically denser medium (substance) towards an optically less dense substance.
If the angle of incidence is large enough (greater than the critical angle ), such that:
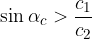
or:
the beam is completely reflected from the boundary surface and no longer penetrates the other substance. Then the law of reflection applies, which says that the angle of incidence is equal to the angle of reflection.
