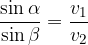Personal collections


Sound is transmitted from the source to the receiver as a longitudinal wave. As with other waves, typical wave phenomena can be observed in sound:
The wave hits a barrier and bounces off. So let's observe the reflection of the wave.
It can also bend around an obstacle so that we can hear the sound even though we can't see the source. The phenomenon is called diffraction.
Multiple sound waves can superimpose on each other. In doing so, they are added or subtracted. The sound increases or decreases. The phenomenon is called wave interference.
Sound can also pass from a solid or liquid to air or vice versa. At the boundary of the two substances, the direction of propagation changes. We say it refracts.
In this material, we will learn more about:
diffraction,
interference, and
refraction.
of sound. The listed phenomena are not only characteristic of sound. They can also be found in other types of waves, e.g. waves of the water surface, light wave, radio waves, etc.
A sound hits an obstacle and is diffracted by it. Instead of just spreading straight (away from the source), it also spreads behind the obstacle into an area that the source can't see. We say that the sound behind the obstacle also propagates into the wave shadow. This is the reason why we hear sound in the open, even though we cannot see the source of the sound because it is blocked by some object.
How much the sound will be diffracted by the obstacle depends on its wavelength. The diffraction is larger at longer wavelengths.
The diffraction of sound can be explained using Huygens' principle. This says that each point of the wavefront (for example, one crest in the wave) is the origin of new, elementary waves. We call them Huygens sources. Elementary waves have a hemispherical shape and propagate forward at the same speed as the original wave. The envelope of these waves forms the next wavefront.
An infinite number of elementary sources are thought to be placed on the entire wavefront that hits the opening in the barrier. These emit hemispherical elementary waves in the direction of propagation of the original wave. The elementary waves add up and the envelope of these waves forms a new wavefront after one wavelength - Figure 3.
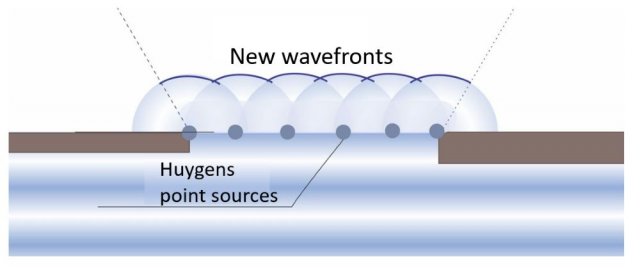
Figure 3: Huygens' principle. Only a few elementary sources are drawn at the place of the opening in the barrier. The more we draw, the more the new wavefront resembles the flat wavefront in front of the obstacle
In the width of the opening, the fronts of elementary sources add up so that the envelope is a straight line. We get a wave, the same as before the obstacle. Right next to the obstacle, the envelope has a hemispherical shape. The wave therefore also propagates behind the obstacle. The maximum angle 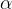 at which it expands depends on the width of the opening. With a wider opening, the angle
at which it expands depends on the width of the opening. With a wider opening, the angle 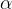 is smaller - Figure 4. If the width of the opening is equal to the wavelength
is smaller - Figure 4. If the width of the opening is equal to the wavelength 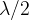 of the wave, the angle is
of the wave, the angle is 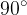 ; the beam is hemispherical.
; the beam is hemispherical.
The width of the opening determines the first attenuation of the wave due to the interference of neighboring elementary sources, which we will see in the next chapter.
Plane waves travel through an opening in a barrier. In the width of the opening, the shape of the wave behind the opening does not change, it remains a flat wave. At both edges, the wave bends. The waves take on a hemispherical shape and propagate behind the edge of the obstacle. The angle at which they spread depends on the width of the opening. The wider the opening, the smaller the diffraction angle. If the opening is equal to 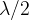 , we get a hemispherical wave of elementary origin.
, we get a hemispherical wave of elementary origin.
Interference between waves occurs when two or more waves meet at the same place. This usually happens when we have multiple sources of waves or when waves bounce off walls. Waves pile on each other therefore creating constructive or destructive interference.
In this chapter, we will assume that two-spaced sources oscillate simultaneously. This can also be achieved by placing a barrier with two narrow openings far from a speaker. Plane wave fronts arrive at the obstacle (see Figure 5). We have seen that each narrow opening becomes the source of a new wave - a Huygens source. These two openings therefore become simultaneous origins of hemispherical waves. Simultaneity means that they cast a crest or a trough at the same time. The waves from both sources add up. We can observe amplification or attenuation of the sound - depending on where we stand behind the obstacle.
Let's imagine that a plane sound wave hits an obstacle in which there are two openings at a distance 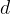 to each other - see Figure 5.
to each other - see Figure 5.
Each opening is the origin of a hemispherical wave. The waves from both sources overlap each other and add up. Far enough away from the obstacle, the crests (or troughs) from both sources always meet at the bisector between the openings. The sound is amplified in this direction - Figure 5.
The sound is also amplified at some other angle 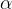 with respect to the vertical (bi-sector) if the condition that two crests or two troughs meet is met. Then, the path difference of the two waves is equal to a multiple of the wavelength and the two waves add up - Figure 6.
with respect to the vertical (bi-sector) if the condition that two crests or two troughs meet is met. Then, the path difference of the two waves is equal to a multiple of the wavelength and the two waves add up - Figure 6.
Let's see for what angle the wave is amplified. In Figure 6, we see a right-angled triangle with:
the interior angle 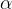 opposite the leg with length
opposite the leg with length 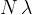 , and
, and
an hypotenuse 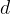 .
.
From this triangle, we have:
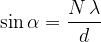
Two sources emit a spherical sound wave with the same frequency. The direction of sound amplification can be calculated using the equation:
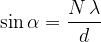
Where 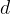 is the distance between the two sources, and
is the distance between the two sources, and 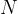 is 0 and natural numbers.
is 0 and natural numbers.
Waves can also be subtracted in a certain direction. In this direction, the sound will be greatly attenuated.
Let's take two narrow openings through which a flat sound wave enters. Each opening is the origin of a hemispherical wave, as shown in Figure 7.
At a certain angle 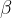 with respect to the perpendicular to the obstacle, the waves are subtracted. This happens when the crest of one wave falls on the trough of another. Then the waves are shifted (Figure 7) by
with respect to the perpendicular to the obstacle, the waves are subtracted. This happens when the crest of one wave falls on the trough of another. Then the waves are shifted (Figure 7) by 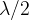 ,
, 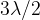 or in general:
or in general:

Where 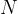 is zero and natural numbers. The condition for this to happen is:
is zero and natural numbers. The condition for this to happen is:
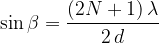
The direction of wave attenuation can be calculated using the equation:
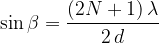
Where 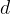 is the distance between the sources and
is the distance between the sources and 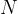 is 0 and natural numbers.
is 0 and natural numbers.
The sound wave travels:
from a medium in which it propagates at a speed 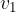
into another medium in which the speed of propagation is  .
.
If the sound does not fall perpendicularly on the boundary of two media, its direction of propagation changes. The phenomenon is called wave refraction. When passing into another medium, the wavelength of the sound also changes.
Let us first assume that the wave is incident perpendicular to the boundary of two media. Let's see how the wavelength 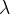 changes.
changes.
In both media, the wave travels a distance 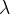 in one period
in one period  :
:


Let's divide equation by 1 by 2:
When a wave passes from one medium to another that has a different wave propagation speed, the wavelength changes:
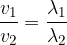
What if the wave beam is not incident perpendicular to the boundary plane?
Let's look at Figure 10. A wave beam hits the boundary surface of two mediums at an angle 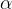 . Let's assume that the speed of the wave in the medium from which the wave is incident is greater than the speed in the medium into which it is refracted.
. Let's assume that the speed of the wave in the medium from which the wave is incident is greater than the speed in the medium into which it is refracted.
Let the wave speed in the first medium be 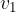 , and in the second medium
, and in the second medium  , and the following applies:
, and the following applies:
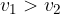
When a wave passes into another medium, it changes its direction of motion. We say it refracts.
Let's look at Figure 10. The wavefronts is incident on the boundary between the two mediums. The wavefront must always be perpendicular to the wave beam. As at the moment the left edge of the wave has already hit the boundary surface, the right edge still has a distance 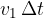 to travel before hitting the boundary.
to travel before hitting the boundary.
The same applies to a wave that has already penetrated the second medium. The left edge of the wavefront has already hit the boundary surface while the right edge still has a distance 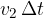 to travel before hitting the boundary.
to travel before hitting the boundary.
Let’s look at the triangle marked along the boundary area.
From the triangles:
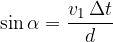
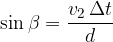
Let's divide both equations:
The law of refraction states that the ratio of the sine of the angle of incidence to the sine of the angle of refraction is equal to the ratio of the speeds of propagation in the two media: