Just as we know multiplication between numbers in mathematics, we also know multiplication between vectors. The multiplication of two vectors is called scalar product. That the definition of multiplication between vectors, as we will write it, is correct, is shown by the fact that it literally merges with other findings in mathematics - e.g. Pythagoras' saying. Pythagoras' theorem is the result of the multiplication of two mutually perpendicular vectors.
Give the vectors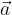 
and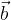 
, which have a common starting point and enclose as 
.
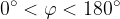The scalar product of the two vectors is equal to the product of the magnitudes of the first and second vectors and the cosine of the intermediate angle:
The result of scalar multiplication is a real number or scalar.
From the scalar product form:
We can quickly figure out when the scalar product is equal to 0. This will be when at least one of the vectors and 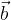will be the zero vector or when 
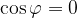. This is when the vectors are perpendicular (
).
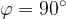If the vector 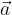is scalarly multiplied by itself, the angle 
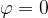is:
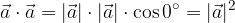
The length of the vector 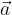is therefore equal to:
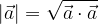
The calculation of the length of the vector given by the components is given in the material Scalar product in the rectangular coordinate system. Here, let’s look at a simple example.
The perpendicular projection of the vector 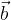on the vector (
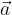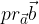) is the line obtained by projecting the start and end points of the vector 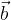perpendicular to the vector .
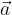When the vector 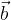is projected at right angles to the vector 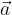, a right triangle with hypotenuse 
and leg 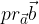is obtained.
In a right triangle, we use the angular function cosine:
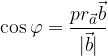
from the obtained connection we express:
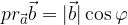
The resulting bond is inserted into the formula for the scalar product:
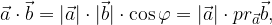
which can be written as:
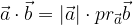
The scalar product of two vectors is equal to the product of the length of the first vector and the orthogonal projection of the second vector onto the first vector.
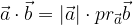
Scalar multiplication is subject to the law of substitution or commutativity:
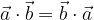
Scalar multiplication is subject to the law of decomposition or distributivity:
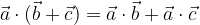
The scalar product is homogeneous:
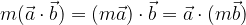
The cosine theorem is often used in solving any triangle. Here we will look at the derivation of a cosine theorem with vectors.
In any triangle, mark the sides with the vectors 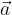, 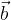and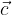 
, and as 
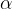(see figure).
The vector 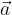is expressed by the vectors 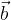and :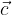
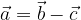
Let's transform the written equation:
We get a cosine theorem. Equivalently, we can derive a cosine theorem for all three sides of the triangle.
The cosine theorems for all three sides in any triangle are:
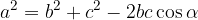
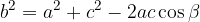
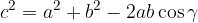
The Pythagorean theorem is only a special form of the cosine theorem. Let’s look at what happens to the cosine theorem if we consider a right triangle where c is the hypotenuse, a and b are the sides:
We derive the Pythagorean theorem from the cosine theorem:
The derivation of the Pythagorean theorem by means of a scalar product (the scalar product was used in the derivation of the cosine theorem) is further proof that the definition of a scalar product, as stated, is the right way to multiply vectors among themselves.
