In the material Scalar product, we generally looked at how we multiply vectors with each other. In this material, we will look at how we perform a scalar product in a rectangular coordinate system.
The scalar product of two vectors, when their lengths and the angle between them are known can be calculated. Now, let’s look at how to calculate the scalar product of the vectors given by the components.
The vectors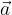 
and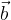 
are given in the three-dimensional rectangular coordinate system with the components:
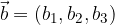
Let’s derive the formula for calculating scalar product:
The scalar product of the vectors and 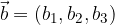in the coordinate system is equal to the sum of the products of the individual components:
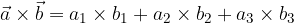
The formula for the length of a vector is derived in the chapter Vectors in the rectangular coordinate system; the same result can also be obtained from this material as well.
Given the vector be , obtain the length of the vector.
Let’s obtain the formula for vector length using the scalar product:
The length of the vector given by the components is calculated by the formula:
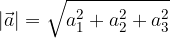
A unit vector is a vector of length 1. Any vector can be assigned a unit vector, but it is used for purely practical purposes.
The unit vector 
of (any) vector is determined by dividing the components of the vector by its length:
