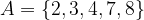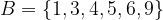A set denotes a group of different elements. Elements of a set can be numbers, letters, vehicles, fruits, etc., which we combine into a set and are connected by some common property.
A set is a group of elements that are united by a certain property. We mark it with capital letters:
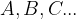
its elements are written in curly brackets.
Each individual unit of a set is called an element of the set.
If the set A contains the element a, this is written with the symbols:
and we read: a is an element of the set A.
If the set A does not contain the element x, write this as:
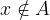
and we read: x is not an element of the set A.
If the set A does not contain any elements, this is written with the symbols:
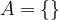
but
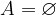
and we say that A is an empty set.
Sets are divided into:
finite (have finite many elements)
infinite (have infinitely many elements)
A universe or universal set is a set from which we choose elements. It can be a finite or an infinite set.
A subset or partial set of the set 
is such a set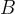 
if each element of the set 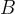is also contained in the set . The set B, which is a subset of the set A, is denoted by:
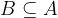
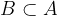
The power set of a set is the set of all its subsets. The elements of a power set are therefore sets. The power set of the set A is denoted by:
The power set is the number of subsets that the set contains. The label is:
and we read: the power of the set A.
Let's add the following statements:
If a set A has n elements, the power set of its set is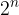 
.
The power of the union of sets A and B is equal to the sum of the power of both sets minus the power of the intersection of the sets (the number of elements contained in both A and B) :
If a set has as many elements as natural numbers, we say that it is countably infinite. Its power is aleph zero (the first letter of the Hebrew alphabet):
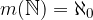
The cardinality of a set refers to the number of elements n a set has.
The sets and 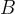are the same if the set is a subset of the set 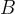, at the same time the set 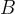is also a subset of the set :
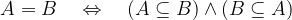
We illustrate the set with Venn diagrams. We denote the universe or universal set by a rectangle, and the sets by closed curves.
Venn diagram
Drawing result:
Venn diagram
Now we can read the solution from the diagram:
