Personal collections


We are already familiar with sets in the material Set notation for KS4. In this material, however, let us look at the operations between them.
The union of two sets is a set that contains all the elements of the first and all the elements of the second set (without repeating any element).
The union of sets A and B is denoted as:
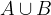
and contains all the elements from both sets.
The intersection of two sets is a set that contains all the elements that are in the first and second sets at the same time.
The intersection of the sets A and B is denoted as:

and contains elements that are in both sets.
Sets that have an empty intersection (i.e.  ) are said to be disjoint sets.
) are said to be disjoint sets.
The difference of two sets is a set that contains all the elements from the first set that are not in the second set.
The difference between the sets A and B is denoted as:

or
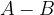
and contains elements from the set A that are not in the set B.
The complement of a set is the set that contains those elements of the universal set that are not contained in the set.
The complement of the set A is denoted as:
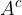
and contains elements from the set U (universal sets) that are not in the set A.
The Cartesian product of sets is the set of all possible ordered pairs, with the first element of the ordered pair being from the first set and the second from the second.
The Cartesian product A and B is denoted as:
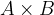
and contains ordered pairs 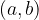 where
where 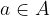 and
and 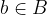 .
.