Let’s look at an example of interest that we often encounter in everyday life.
The content of the above example is certainly familiar to us from everyday life, and the terminology used may be foreign to us. So let’s look at the explanation of the terms used.
The loan amount is called principal or capital. Denoted as P.
The amount we have to repay in addition to the principal is called interest. Denoted as I.
Interest rate is the amount expressed as a percentage, which is attributed to the principal after a certain period of interest. Denoted as R (in %).
We usually bear interest at an annual interest rate, which means that we accrue interest on the principal at the end of each year.
Interest period is the period in which interest is accrued on the principal. Denoted as T or n.
The annual interest period is also called the basic interest period.
If the interest period is less than one year, its basic unit is a day or a month:
If the base unit is a day, in a normal year the day represents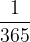 
annual interest periods, and in a leap year 
.
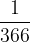If the base unit is a month, then the month represents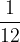 
annual interest periods.
Any savings or loan repayments expire or end after a certain period of time.
The entire repayment period is called interest rate, and is the period in which the amount is remunerated.
When we borrow an amount from a financial institution, we talk about repaying a debt, which consists of:
actual amount received (principal)
and the interest we pay so that we can borrow that money.
When we invest an amount in a financial institution, we talk about a deposit. The amount obtained after a certain period consists of:
the actual amount invested (principal)
and the interest given to us by the financial institution because we invested our money in it.
The amount of interest always depends on the following factors:
main or initial capital
duration of interest
interest rates
In our daily lives, we often encounter such business money when we save, rent and repay credit, make a profit and the like. The process of such business is called interest.
Most often we encounter a simple interest and compound interest, which can be solved as a mathematical problem using an arithmetic and geometric sequence.
Ordinary or simple interest is interest in which only the initial capital without added interest is remunerated at all times. This means that the amount of capital increases by the same monetary value in each interest period.
The interest obtained in ordinary interest on the principal P, which is usually remunerated for T years at an R% interest rate, is recorded as:
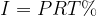
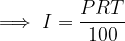
In ordinary interest, the initial capital always increases linearly, which is why it is also called linear interest. This means that after 1, 2, ..., n years and taking into account that in a simple interest period the principal P increases by the same amount of interest, the principal values are:
After n years, the amount of capital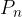 
for linear interest is:
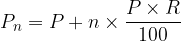
The interest procedure is illustrated on a graph for the amount P = £10 000 and the interest rate R = 5%:
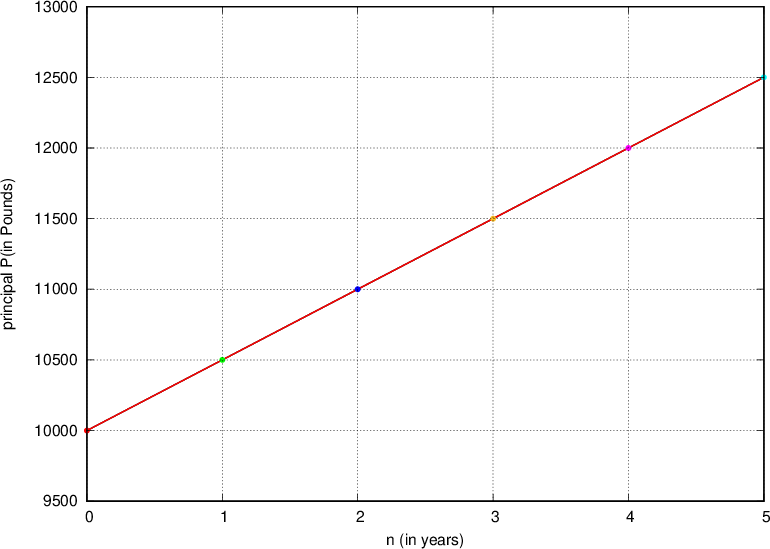
Obviously, the interest is really linear (the graph is a straight line), and the successive values of the principal make up the arithmetic sequence.
Note: Ordinary interest is very rarely used in money transactions today.
A Compound interest rate is the interest rate in which, in addition to the initial capital, interest is also paid. This means that in each interest period the interest received is added to the principal and in the subsequent interest period the principal is accrued with the added interest from the previous period.
Interest rates yield higher interest rates than ordinary interest rates, as instead of principal, capital is essentially paid in interest, which increases with the end of each interest period.
Let's calculate the interest if we have the principal P for n years with R% annual compound interest rate:
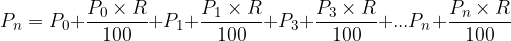
We consider:
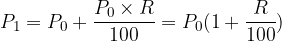
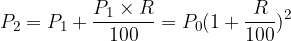
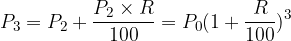
and we get:
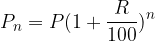
We note that all principal values have a common sequence quotient of the form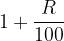 
, which is called the annual interest rate factor.
The annual interest rate factor is denoted by r:
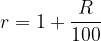
We write the value of the principal P in another way.
We know that:
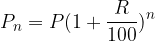
We introduce the interest rate factor and get:
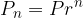
For compound interest rates, the initial capital always grows exponentially. This means that after 1, 2, ..., n years and taking into account that in an individual interest period the principal P increases by the interest obtained in the previous period, the principal values are:
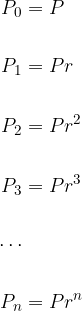
The interest procedure is illustrated on the graph for the amount P = £1000 and the interest rate R = 8%:
Obviously, the interest is really exponential, and the successive values of the principal make up a geometric sequence with a common ratio r. The principal increases the faster, the higher the value of r or the higher the interest rate R.
Usually, in practice, we define the annual interest rate for interest rates. However, the interest rate can also be converted into shorter periods of time (half-year period or at the end of each month and even day).
At the semi-annual compound interest rate, interest is added to the principal after 6 months of interest, which is then, together with the principal, accrued onwards, for the next 6 months.
Thus, the semi-annual interest rate is equal to:
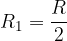
At the monthly compound interest rate, the principal is accrued on a monthly basis, which is then accrued together with the principal, in the following month.
Monthly interest rate is equal to:
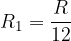
When we have a semi-annual / quarterly / monthly / daily interest period and a semi-annual / quarterly / monthly / daily compound interest rate, then it is considered that:
The principal in m half-years / quarters / months / days increases to:
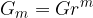
where the interest factor is:
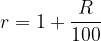
Anticipatory interest - a method of interest in which the lender calculates interest at the beginning of the period and deducts it from the nominal value of the principal.
Time of interest - time period in which we save or. we repay.
Debt - the amount consisting of the principal and interest that is owed.
Principal or initial capital - the amount of money saved and invested.
Annual interest rate - tells us what percentage of the amount paid or received is interest on an annual basis. This is expressed in percentages.
Linear interest - a method for calculating interest, in which we use a simple interest account.
Simple interest - a method where interest is calculated from the original principal only.
Interest - the amount by which the value of the principal is increased. We can also say that interest is compensation for the use of a certain amount of money.
Interest rate - the amount we pay for borrowed money or the income we get from saving. We express it in percentages.
Interest period - the period at the end of which interest is credited to the principal. The usual interest period is month, quarter, semester, one year.
Compound interest rate - a method at which the interest is added to the principal after each period. The principal with accrued interest is accrued each time.
Interest rate factor - based on the interest rate on the interest rate.
Installment or annuity - is the amount we pay to the lender in certain time periods when repaying the debt.
Deposit - the amount we invest in a financial institution.
