Personal collections


Pendulums can swing in several possible ways. In this chapter, we will consider periodic oscillation, when the displacement of the pendulum from the equilibrium position is a sine function of time. This oscillation is called harmonic oscillation.
In nature, we have a very rare example of an ideal harmonic oscillation. The shape of the oscillation is most often a distorted sine wave, but it can always be mathematically resolved into the sum of harmonic oscillations. That is why we call harmonic oscillation also fundamental oscillation.
Let us imagine the oscillation of a weight attached to a light inextensible string as shown in the figure. This is a simple pendulum.
The pendulum is initially at rest in the equilibrium position. It only swings if we add energy to it. When we move it out of the equilibrium position, raise it to a height so that it has potential energy, and then release it, the pendulum begins to fall and its potential energy is gradually transformed into kinetic energy. It reaches the maximum kinetic energy and thus the maximum speed  in the equilibrium position.
in the equilibrium position.
The pendulum then being to rise again and Its energy is then gradually converted back into potential energy and reaches the maximum potential energy and hence the maximum height at the other end of its oscillation. The process is then repeated in reverse.
If there are no energy losses, the sum of both energies in all positions of the pendulum is the same. It is called the total energy of the pendulum.
In the next section, we will see that harmonic oscillation is actually a projection of a rotation onto the axis of a rectangular coordinate system which represents the deviation from the equilibrium position.
Definitions:
The equilibrium position of a pendulum is the position at which an unexcited pendulum would rest.
The amplitude 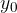 of oscillation is the maximum deviation of the pendulum from the equilibrium position.
of oscillation is the maximum deviation of the pendulum from the equilibrium position.
The oscillation period 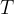 is the time it takes for the pendulum to return to its initial position after the oscillation.
is the time it takes for the pendulum to return to its initial position after the oscillation.
The oscillation frequency 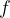 is the reciprocal of the oscillation period
is the reciprocal of the oscillation period 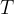 . It tells us how many complete oscillations the pendulum makes per second.
. It tells us how many complete oscillations the pendulum makes per second.
Harmonic or sinusoidal oscillation of a pendulum is a case where the instantaneous displacement from the equilibrium position is a sine function of time.
The simple pendulum mentioned in the introduction is only a conditional harmonic pendulum. In the material, Pendulum, we will see that it oscillates approximately sinusoidally only if the amplitude of the oscillation is small enough compared to the length of the string.
Let's observe the displacement from the equilibrium position, the speed, and the acceleration in harmonic oscillation. The start of the observation can be arbitrary. We assume we observe the oscillation from the moment the pendulum passes through the equilibrium position.
Imagine the oscillation of an ideal harmonic pendulum as a projection of a rotation on the 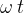 , y coordinate system, as shown in the figure below:
, y coordinate system, as shown in the figure below:
Let's take a point on the circumference of the circle with radius 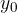 . The point circles in a counter-clockwise direction and describes the angle
. The point circles in a counter-clockwise direction and describes the angle 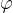 which is given as:
which is given as:
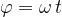
The projection of a point on the circle onto the y-axis describes the instantaneous value  of the displacement from the equilibrium position of the harmonic pendulum:
of the displacement from the equilibrium position of the harmonic pendulum:

The speed 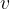 of the oscillation is the derivative of the displacement from the equilibrium position over time. If we have not yet mastered the derivation, we imagine the velocity as the slope of the displacement-time graph:
of the oscillation is the derivative of the displacement from the equilibrium position over time. If we have not yet mastered the derivation, we imagine the velocity as the slope of the displacement-time graph:

From the graph above, we can see that the slope of y (t) is greatest in the equilibrium position. The function that describes the slope of a sine function is the cosine function:

The speed is therefore greatest in the equilibrium position. It is proportional to the angular velocity 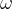 and maximum displacement (amplitude)
and maximum displacement (amplitude) 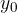 . Mathematically, more advanced scholars can prove this using calculus.
. Mathematically, more advanced scholars can prove this using calculus.
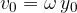
The acceleration  of the oscillation is the derivative of the velocity over time. If we haven't mastered derivation yet, we imagine acceleration as the slope of a graph of velocity over time. On the velocity-time graph, it can be seen that the slope is greatest at the maximum displacement from the equilibrium position.
of the oscillation is the derivative of the velocity over time. If we haven't mastered derivation yet, we imagine acceleration as the slope of a graph of velocity over time. On the velocity-time graph, it can be seen that the slope is greatest at the maximum displacement from the equilibrium position.

Without a mathematical explanation, we write:
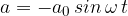
The peak value of acceleration (maximum acceleration) 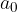 is proportional to the maximum velocity
is proportional to the maximum velocity  and angular velocity
and angular velocity 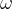 . The more mathematically advanced scholars can show this using calculus - see the next section. The acceleration is greatest in the position when the oscillation speed is zero, i.e. at the maximum displacement from the equilibrium position.
. The more mathematically advanced scholars can show this using calculus - see the next section. The acceleration is greatest in the position when the oscillation speed is zero, i.e. at the maximum displacement from the equilibrium position.

The displacement  from the equilibrium position of a harmonic pendulum from the moment it passes through the equilibrium position is given by the equation:
from the equilibrium position of a harmonic pendulum from the moment it passes through the equilibrium position is given by the equation:
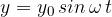
The oscillation speed 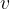 is given as:
is given as:
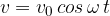
The maximum speed  is in the equilibrium position (y = 0) and is given as:
is in the equilibrium position (y = 0) and is given as:
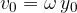
The acceleration  of oscillation is given as:
of oscillation is given as:
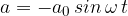
The maximum value 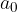 of the acceleration is at the maximum displacement from the equilibrium position and is given as:
of the acceleration is at the maximum displacement from the equilibrium position and is given as:
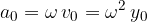
This section is intended for students who have already mastered calculus. Students with no knowledge of calculus can safely skip this section.
The notation  is often used in high school as a substitute for the notation
is often used in high school as a substitute for the notation  .
. 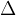 means a difference (e.g. time difference), and this difference can be arbitrarily large. The notation
means a difference (e.g. time difference), and this difference can be arbitrarily large. The notation 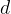 , like
, like 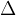 , also means a difference, but only an infinitesimal difference.
, also means a difference, but only an infinitesimal difference.
In order to get the velocity 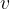 as the derivative of the displacement over time, we first replace the notation
as the derivative of the displacement over time, we first replace the notation 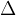 in equation (2) with
in equation (2) with 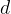 :
:
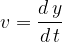
The displacement  is the sine function of time. Equation (1) is therefore derived according to the rules of differentiation to get:
is the sine function of time. Equation (1) is therefore derived according to the rules of differentiation to get:
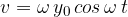
The factor  represents the maximum speed
represents the maximum speed  :
:
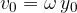
Similarly, we calculate the acceleration as the derivative of velocity over time. For this purpose, we replace the notation  in equation (3) with
in equation (3) with  :
:
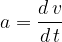
The velocity 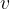 is a cosine function of time. Equation (3) is therefore derived according to the rules of differentiation to get:
is a cosine function of time. Equation (3) is therefore derived according to the rules of differentiation to get:
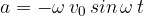
The factor  represents the maximum acceleration
represents the maximum acceleration 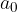 :
:
