A uniform beam is clamped at one end. A metal block of mass m is fixed to the other end of the beam causing it to bend, as shown in the figure below.
The block is given a small vertical displacement and then released so that it oscillates with simple harmonic motion. The acceleration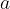 
of the block is given by the expression
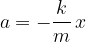
where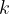 
is a constant for the beam and 
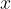is the vertical displacement of the block from its equilibrium position.
For the beam,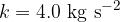 
. Show that the angular frequency 
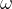of the oscillations is given by the expression
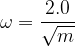
The initial amplitude of the oscillation of the block is 
. Use the expression in (a) to determine the maximum kinetic energy of the oscillations.
Over a certain interval of time, the maximum kinetic energy of the oscillations in (b) is reduced by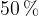 
. It may be assumed that there is negligible change in the angular frequency of the oscillations. Determine the amplitude of oscillation.
Permanent magnets are now positioned so that the metal block oscillates between the poles, as shown in the figure below.
The block is made to oscillate with the same initial amplitude as in (b). Use energy conservation to explain why the energy of the oscillations decreases more rapidly than in (c).
.
.
