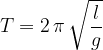Personal collections


A simple pendulum is a theoretical pendulum because it assumes that the weight of the string on which the bob oscillates is zero. The results of the calculations of the oscillation frequency also apply approximately to real pendulums, where it oscillates:
dimensionally small bob;
on threads with a mass much less than that of the bob;
with small amplitude.
We have a bob hanging from a light string. We move it out of its equilibrium position for a maximum displacement and give it potential energy. When the bob is released, the potential energy is converted into kinetic energy and then again into potential energy. The bob oscillates around the equilibrium position, that is, the point in the lowest position of the oscillation.
A simple pendulum is approximately a harmonic (sine) pendulum only for small oscillation amplitudes, which we will show when deriving the oscillation frequency.
Let's calculate the frequency and oscillation period of the described pendulum:
In the case of a maximum displacement  , a force acts on the bob in the opposite direction of the original displacement, the force is therefore negative:
, a force acts on the bob in the opposite direction of the original displacement, the force is therefore negative:
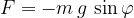
or acceleration:

The maximum displacement (amplitude)  from the equilibrium position is the length of an arc of a circle with radius
from the equilibrium position is the length of an arc of a circle with radius 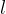 and angle
and angle 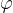 :
:
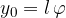
Let's make 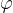 the subject of the equation:
the subject of the equation:
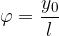
Let's insert the result above in Equation 2:
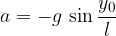
Let's recall that in harmonic oscillation, the acceleration is proportional to the maximum displacement (amplitude) from the equilibrium position:

and not its sinusoidal value.
In our case, it will be approximately proportional only for small angles, when the sine of the angle is equal to the angle:

Let's therefore equate the expressions on the right-hand sides of equations 3 and 4:
The formula of the oscillation period 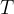 includes the length
includes the length 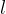 of the string and the acceleration due to gravity
of the string and the acceleration due to gravity 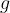 , but no mass. This does not mean, however, that the pendulum would oscillate even without mass because in this case there would also be no force of gravity, which enables it to oscillate.
, but no mass. This does not mean, however, that the pendulum would oscillate even without mass because in this case there would also be no force of gravity, which enables it to oscillate.
A simple pendulum has an angular frequency:
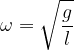
frequency:
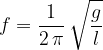
and oscillation period: