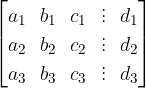Personal collections


A linear equation is obtained when we connect two linear expressions with an equation in which an unknown quantity occurs on the first power. An unknown quantity is usually denoted by x.
In mathematics, a linear equation is an equation in which the highest power of the variable or unknown is 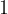 . It is symbolically written as:
. It is symbolically written as:
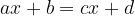
where 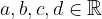
Solving problems from everyday life requires a little more effort from us, as we must first translate them into mathematical language. When we solve the equations, it means that we look for all such values of the unknown x for which the expression is true. Here are the following points:
Understanding the problem
We must first understand the problem. We need to understand what is unknown (variable) and what is constant, what data is available, what the conditions are, and what we need to pay attention to.
Write the equation
We find the connection between the data and the variables. It can help us to remember similar problems that we have already solved.
Solve the equation or system of equations
From the equation we express the unknowns. Our goal is to write down the unknowns with the help of as few other unknowns as possible (if possible with zero unknowns as well). Usually, solving equations or systems of equations is a long process, so it is important to check each step of the solution.
Check the obtained solution
We insert the solution into the original equation. Sometimes, with logical consideration, we can determine whether the solution is correct or contradictory. For many tasks, the result can be assessed by heart. We check the arithmetic by inserting the solution into the equation and in the end the equality must match. Where the result can be calculated in several ways, the results must match each other.
To make it easier to understand the above point, let's show a real example:
When solving equations, we sometimes run into problems. Let's look at two examples:
To make it easier to understand, let's look at the following example:
Using the above calculation, we notice that the equality holds, but we do not have an expressed unknown x. Such an equation is called an identical equation, and its solution is any real number.
Here, too, for easier understanding, let us look at the following example:
Using the above calculation, we find that the unknowns are annihilated and we get an equality that cannot be valid for any real number, so this equation has no solution.
If we add or subtract the same number on both sides in a linear equation, or multiply or divide both sides by the same non-zero number, we get an equivalent (equivalent) equation, that is, an equation that has the same solutions as the original equation.
With the current knowledge, we will also be able to solve some quadratic equations or equations of higher degrees. These are equations in which a variable appears with a second or even higher power. We deal with such equations as follows:
Equation transformations
With basic operations, we transform the equation into an equivalent equation that has all the terms on the left-hand and only zero remains on the right-hand.
Merge equivalent terms
Which means that we calculate the equation (terms that are all on the same degree).
Split the expression into linear terms
The calculated left-hand side (if possible) is split into the linear factors themselves.
Consideration of individual terms
We equate each of the split (at best linear) terms with zero. Namely, we know that the product of (linear) factors is equal to 0 only if at least one of the factors is equal to 0:
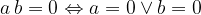
Following the above procedure, the quadratic equation is translated into two linear equations, the third degree equation is translated into three linear equations, and so on. The equation has as many solutions as its degree. Such an equation is called a split equation.
First, let's look at the form of a system of two linear equations:
The system of two linear equations with two unknowns x and y is of the form:
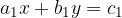
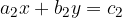
where:
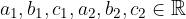
To solve a system of two linear equations means to find such values for the unknowns x and y that both equations of the system will suffice. The system of equations can be solved in several ways, we will look at two below.
The system of two equations with two unknowns is solved in an interchangeable way by expressing one unknown from an arbitrarily selected equation. We then insert the expressed instead of this unknown into the rest of the equation.
This is how we get rid of the expressed unknown. We get one equation with one unknown that is not difficult to solve. Then we just calculate the missing unknown.
The principle for solving a system of two equations with two unknowns using the method of elimination is as follows:
We multiply one or both equations to get the same coefficients in front of the same unknown in both equations.
The equation is then summed and one unknown is excluded.
We Calculate the value of the excluded unknown.
Note:When solving problems from everyday life, we must first translate them into mathematical language, and then it is time to solve systems of equations.
Several strangers may also be involved in the problem. If we are looking for a value for three unknowns, we need three equations. First, let's look at the form of a system of three linear equations:
The system of two linear equations with two unknowns x and y is of the form:
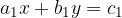
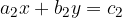
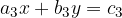
where 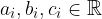 and
and 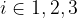
We solve such systems similarly to systems of two equations with two unknowns. Swap mode is exactly the same, except that in this case the expressed unknown is inserted into the equation, where we re-express the unknown, which is inserted into the original equation. Let's take a closer look at the Elimination method.
As we already know, we have to multiply the equations by certain numbers and add them together so that one of the unknowns "is eliminated". For better transparency, we write numbers before the unknown (coefficients) in matrices (the order of the equations can be changed). The matrix is generally of the following form: