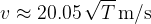Personal collections


Sound is a longitudinal wave of air particles.
As an example, let's take a loudspeaker as a sound source: when the diaphragm moves to the right of the rest position A (see the figure below), a compression of air molecules (higher air density) is created and, as a result, there is an increase in air pressure. As the diaphragm moves to the left, it causes rarefaction (the density of the air decreases) and a decrease in air pressure. The oscillation 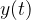 of the diaphragm overtakes
of the diaphragm overtakes 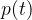 by an angle
by an angle 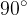 , as shown in the figure:
, as shown in the figure:
On the receiving side, the process is reversed: increased and decreased air pressure causes the eardrum or microphone diaphragm to oscillate.
A longitudinal wave of air particles is the oscillation of particles in the direction of wave propagation. As a result of longitudinal waves, the air thins and thickens, and the air pressure increases and decreases.
The sound we can hear is in the frequency range of 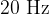 to
to 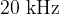 . Sound with lower frequencies is infrasound, and with higher frequencies is ultrasound.
. Sound with lower frequencies is infrasound, and with higher frequencies is ultrasound.
Compressions and rarefactions spread to the surroundings with the speed of sound  . In time
. In time 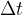 , they travel a distance
, they travel a distance 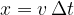 , and in the time period
, and in the time period 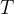 of one oscillation, a distance equal to one wavelength
of one oscillation, a distance equal to one wavelength 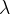 of the wave is covered:
of the wave is covered:
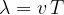
We note that the time period 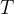 is the reciprocal of the frequency
is the reciprocal of the frequency 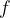 :
:

Therefore;

At a given frequency, the wavelength 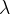 will depend only on the speed of sound
will depend only on the speed of sound  . From equation (1), we also express the frequency
. From equation (1), we also express the frequency 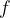 as:
as:
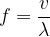
The pressure 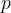 caused by a travelling sound wave depends on distance
caused by a travelling sound wave depends on distance 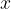 and time
and time 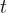 . We write this in the form:
. We write this in the form:
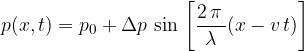
Sound travels not only through air but through any substance that can be compressed under the influence of pressure. The compressibility 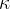 of the substance is calculated according to the equation:
of the substance is calculated according to the equation:
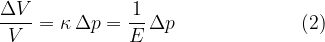
The compressibility 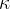 of a substance and the modulus of elasticity
of a substance and the modulus of elasticity 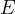 are inversely proportional.
are inversely proportional.
We derived the wave speed  in the material, Progressive transverse wave and it is given as:
in the material, Progressive transverse wave and it is given as:

We note from equation 2 that:
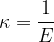
Therefore:
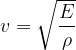
The speed of sound in air is calculated using equation (3) and the gas laws. Let's write down the result without derivation:

Where 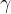 is the ratio of the specific heat capacity
is the ratio of the specific heat capacity 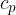 at constant pressure to the specific heat capacity
at constant pressure to the specific heat capacity  at constant volume, this is called adiabatic index. In the case of diatomic molecules, of which air is mainly composed, its value is 1.40.
at constant volume, this is called adiabatic index. In the case of diatomic molecules, of which air is mainly composed, its value is 1.40.
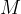 is the kilomolar mass of air (
is the kilomolar mass of air ( ),
),  is the general gas constant and
is the general gas constant and 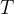 is the absolute temperature in Kelvin.
is the absolute temperature in Kelvin.
We see that in air, the speed of sound is proportional to the root of the absolute temperature. The proportionality constant is calculated from equation (4) and we get: