Personal collections


The square of the number is already known.
Let's see what the square of the binomial looks like:
Let’s take a look at how we calculate it below.
We get to the square of a binomial by the same procedure as multiplying the polynomials. We square a binomial by multiplying it by itself.
When squaring a two-term, we got a three-term. Which are the product of two terms:
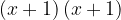
is transformed into the sum of three terms:
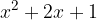
The process of transforming a product into a sum is called expansion.
From the above example, we can understand the rule for calculating the square of a binomial. As a result, we see that for a three-term:
The first term of the trinomial is obtained by squaring the first term of the initial binomial;
The second (intermediate) term of the trinomial is the sum of two identical products - the products of the first and second term of the binomial;
The third term of a trinomial is obtained by squaring the second term of the binomial.
When we calculate the square of a two-term, we always get a three-term.
Derive a general formula for squaring any binomial. Square the binomial , where a and b can be arbitrary numbers (even negative ones).
Let's calculate:
Since the numbers a and b are arbitrary numbers, the above result applies generally, in any case. a represents the first term of the binomial, b the second term. In words, we can form a rule for the square of a binomial as:
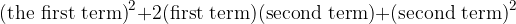
That is, in mathematical form with a form (formula) for the square of a binomial.
We get the rule for calculating the square of a binomial:
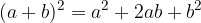
Transforming the product of the terms into the sum or difference of the terms is called factorization.
Let’s look at another example where one of the numbers is negative.
If one of the terms in a two-term is negative, then the result is a three-term that has the second term negative.