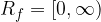A square root function is described as pictured in the diagram below:
where the radicand, a(x), is an algebraic expression. In this material, we shall consider radicands of simple linear expressions.
Having identified a few examples of square root functions, let's now look at evaluating them. To evaluate a square root function f(x), we substitute the given values for x in the function.
Let's examine the graph of the basic square root function:
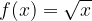
This will help us concretise the concept.
In order to understand the square root function, we need to be able to draw the function's graph. This is done using tabulation. And that means we calculate several plot points, put them in the coordinate system and then draw the curve through the points.
Now, let's tabulate the function f. We obtain the values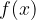 
of the function for some values of x.
We plot the graph of the function f:
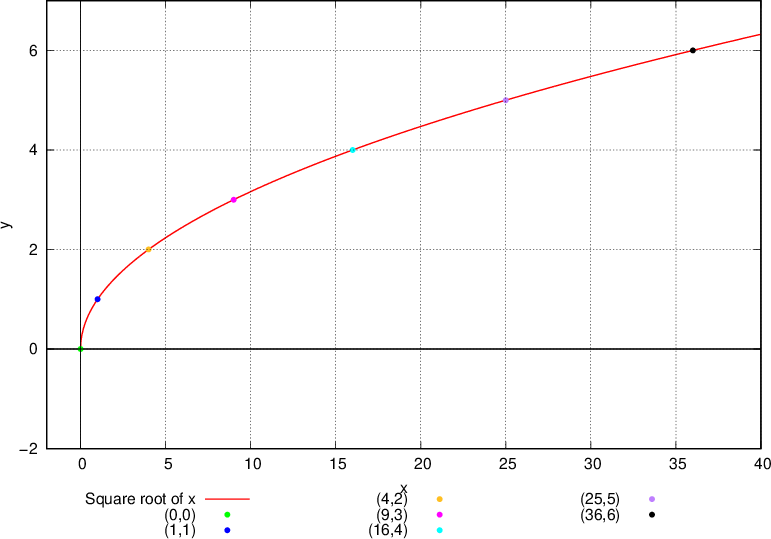
From the diagram above we can observe that the graph of 
is parabolic and covers both:
whole of the positive x axis and
the positive y axis.
The domain and range of a square root function describe the regions where the square root functions exist. Here, we shall examine how the domain and range of specifically the basic square root function,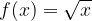 
, and generally other square root functions, 
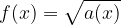, can be obtained numerically and graphically.
We will explore the properties and graphs of general and more complex radical functions in material Radical Functions.
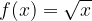
Observing the graph of the basic square root function drawn above, the following properties can be deduced for its domain and range.
Firstly, the domain of the basic square root function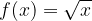 
is the set of all positive real numbers including zero. This is because all real numbers except the negative real numbers can act as a radicand. For a negative real number as a radicand, the value of such a square root function is undefined in real numbers.
Mathematically, the domain of the basic square root function, denoted as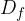 
, is written as an interval in the form:
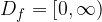
We can also denote the above interval as a set like this:
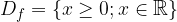
The range of the basic square root function in the set of all positive real numbers including zero, too. This is because the square root of every positive real number is also a positive real number and that of zero is still zero.
Hence, mathematically, the range of the basic square root function, denoted as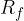 
, is written as:
The domain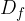 
of the basic square root function 
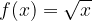is a set of values x which are greater or equal to zero:
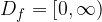
The range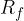 
of the basic square root function 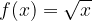is a set of all values 
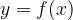of the function. These are all positive real numbers including zero:
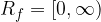
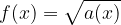
The domain of any square root function can be examined graphically or numerically. Let's see to both approaches.
Graphical Approach of Obtaining the Domain of a Square Root Function
Graphically, the domain of a square root function is the region of the x-axis where the square root function can be drawn.
Numerical Approach of Obtaining the Domain of a Square Root Function
Recall that the square root of a negative radicand is not a real number. Hence, the domain of a square root function is a set of values for which its radicand is greater or equal to zero:
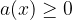
The domain 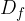of a square root function 
is a set of values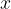 
for which the radicand 
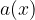is greater or equal to zero:
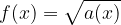
The range of a square root function can be obtained graphically or numerically.
Graphical Approach of Obtaining the Range of a Square Root Function
The range of a square root function is defined as the region of the y-axis which the square root function covers.
Numerical Approach of Obtaining the Range of a Square Root Function
The range of a square root function is the set of values of a square root function. This can be obtained by substituting the boundary values of the domain into the square root function.
The range of a square root function is a set of all values of the function. These are all positive real numbers including zero:
