Personal collections


We excite a wave on a clamped elastic rope by swinging the rope on one side. The wave travels to the end of the rope where it bounces. The summation (superposition) of the incident and reflected waves occurs.
In a special case, it seems to us that the wave is stationary. The length of the rope or any other elastic medium used is then in exact proportion to the wavelength. The maximum amplitude of the rope oscillation is always at the same level and it is called the antinode.
Stationary (standing) transverse waves are found in various musical instruments with string (guitar, violin), elastic membrane (drum), or instruments with elastic wooden or metal plates (xylophone, vibraphone). The string or elastic plate can be rigidly clamped at both ends, at one end, or both ends are not clamped - see Figure 1.

Figure 1: A guitar is an example of a clamped string at both ends, followed by an instrument model with unilaterally clamped elastic tabs, and finally a xylophone with no clamped wooden plates
Before we get to know more about stationary (standing) transverse waves, let’s first look at how a wave bounces off an obstacle.
How the wave will bounce depends on whether the rope is attached at the other end or can move - e.g. by means of a pulley sliding along a horizontal or vertical bar.
If the rope is attached to the wall as shown in Figure 2, the wave is bounced, and consequently, both the incident and reflected waves are in antiphase, i.e., the crest of one is against the trough of the other.
If the rope is attached to the side of the bounce e.g. on a moving pulley, as shown in Figure 3, the wave is reflected, and consequently, both the incident and reflected waves are in phase.
This means the crest of one is against the crest of the other while the trough of one is against the trough of the other.
Therefore, the pulley to which the rope is attached follows the oscillation of the rope.
But what happens if we swing a rope that is clamped on both sides? The rope swings to make it look as if the wave is at rest. We are talking about a stationary (standing) transverse wave. The frequency with which the rope oscillates is called the natural frequency of oscillation of the tensioned rope.
Let us examine standing waves in a case where the length of the rope is a multiple of the wavelength. At the point where the rope is clamped, the wave is reflected in antiphase. At first glance, it seems that the advancing and repulsive waves will be nullified. In reality, however, each piece of rope oscillates with the frequency 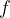 in the direction of the y-axis - see Figure 4 and with the amplitude, which depends on the distance x. In superficial observation, we see only different wave amplitudes depending on the distance x, distributed along the sine function of the distance x. It looks like the wave is standing - Figure 4.
in the direction of the y-axis - see Figure 4 and with the amplitude, which depends on the distance x. In superficial observation, we see only different wave amplitudes depending on the distance x, distributed along the sine function of the distance x. It looks like the wave is standing - Figure 4.
The phenomenon can also be examined mathematically.
This part of the chapter is more challenging and intended for those who would like to know more. It is not essential to understand this part of the chapter.
In the chapter, Progressive transverse wave, we learned the mathematical notation of a travelling sine wave.
The incident wave propagates in the direction of the x-axis toward the obstacle. The wave should have an amplitude of 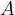 . Then the reflected wave of the same frequency and amplitude comes in the opposite direction. Depending on the mutual phase shift, the waves either add up or subtract. When they add up, the crest of the wave at a given distance x will have a double amplitude, i.e.
. Then the reflected wave of the same frequency and amplitude comes in the opposite direction. Depending on the mutual phase shift, the waves either add up or subtract. When they add up, the crest of the wave at a given distance x will have a double amplitude, i.e. 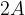 . When the waves are in antiphase, the entire rope will be at rest. At some distance x, the rope will always be at rest - this is the node of the wave.
. When the waves are in antiphase, the entire rope will be at rest. At some distance x, the rope will always be at rest - this is the node of the wave.
Let us now express the incident wave mathematically - see Progressive transverse wave:
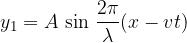
The wave hits an obstacle and bounces off-phase (if the incident wave is a sine function, the reflected wave is a negative sine function). It propagates in the opposite direction to the incident wave (i.e. in the -x direction). Suppose that at the point of reflection the wave goes exactly through the equilibrium position:
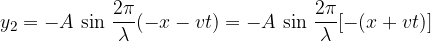
Since 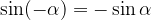 (see oddity of the sine function), we can write the above expression as:
(see oddity of the sine function), we can write the above expression as:
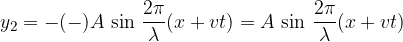
The incident and reflected waves are added together on the rope:

Let's see how the waves add up:
Now, we write the obtained equation in the form:
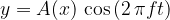
where 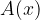 is the amplitude of the oscillation of an observed particle at a distance x from the beginning of the rope. It depends only on the distance x and not on the time t. This is actually the wave envelope we see as a standing wave (see Figure 4):
is the amplitude of the oscillation of an observed particle at a distance x from the beginning of the rope. It depends only on the distance x and not on the time t. This is actually the wave envelope we see as a standing wave (see Figure 4):
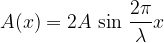
The factor 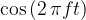 , on the other hand, represents the oscillation of a particle of the string in the direction of the y-axis, which occurs at a certain point x.
, on the other hand, represents the oscillation of a particle of the string in the direction of the y-axis, which occurs at a certain point x.
A standing wave is described by the equation:
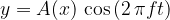
where the amplitude of the wave - or its envelope - A (x)depends on the coordinate x:
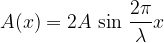
The calculated wave is shown in Figure 4. In fact, only the envelope of the wave A (x) is shown. An oscillation in the y-axis direction is also indicated in the form of vertical lines with arrows indicating the direction of the oscillation.
The fundamental oscillation frequency of a tensioned rope is the lowest frequency when a standing wave is established. The rope can also swing with multiples of this frequency. We call them higher harmonic frequencies.
The fundamental oscillation frequency of a tensioned rope depends on the wave speed, the length of the rope, and the way the rope is clamped.
We tighten the rope and clamp it rigidly on both sides and then swing it with our fingers. The rope oscillates at the fundamental frequency or one of the higher harmonic components. For ease of illustration, we can imagine that we consider the case of string oscillation on a guitar as in Figure 1.
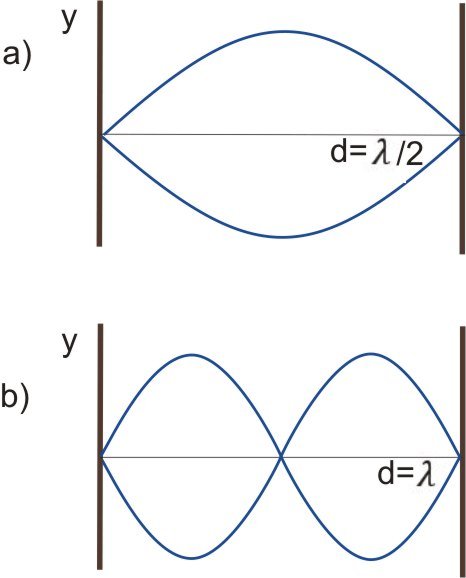
Figure 5: A rope with length d fastened on the sides; a) the fundamental oscillation frequency is shown b) the first harmonic frequency is shown
From Figure 5, we see that for the fundamental frequency, the length 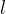 of the rope will be equal to half of the wavelength:
of the rope will be equal to half of the wavelength:
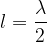
For the first harmonic frequency, the length of the rope will be:
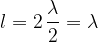
For the second harmonic frequency, the length of the rope will be:
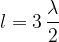
etc .. In general, a standing wave will be established when the length 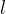 of the rope is a multiple of half a wavelength:
of the rope is a multiple of half a wavelength:
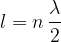
or, if we express in terms of the wavelength:

where 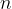 is a natural number
is a natural number 
The wavelength of a standing wave in a rope clamped at both ends is calculated by the equation:
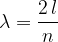
where 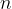 is the harmony (a multiple of the fundamental frequency), and
is the harmony (a multiple of the fundamental frequency), and 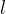 is the length of the rope.
is the length of the rope.
Let's calculate the oscillation frequency:
If 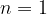 , we get the fundamental oscillation frequency (fundamental tone if it is a musical instrument), if
, we get the fundamental oscillation frequency (fundamental tone if it is a musical instrument), if 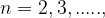 etc., we get higher harmonic components.
etc., we get higher harmonic components.
Instead of a rope, we take an elastic plate, clamp it rigidly on one side, and let it swing freely on the other side (see Fig. 1 middle instrument). We swing the plate with our fingers. The standing wave to be established is shown in Figure 6.
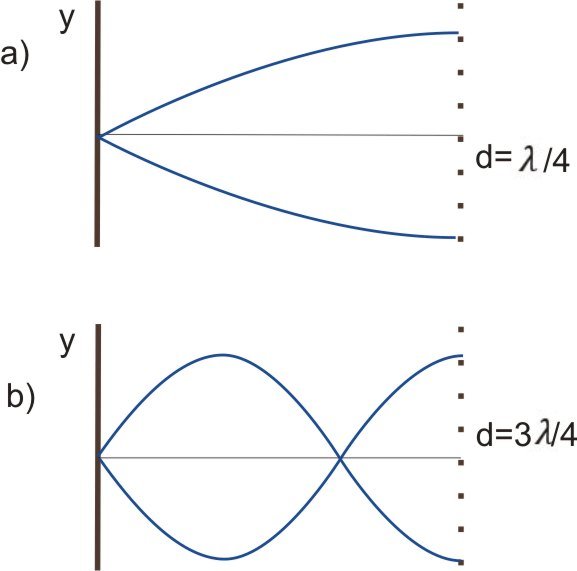
Figure 6: Elastic plate clamped on one side - a) the fundamental oscillation frequency is shown b) the first harmonic frequency is shown
From Figure 6, we see that for the fundamental frequency, the length 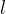 of the rope will be equal to a quarter of the wavelength:
of the rope will be equal to a quarter of the wavelength:
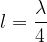
For the first harmonic frequency, the length of the rope will be:
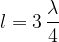
For the second harmonic frequency, the length of the rope will be:
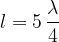
etc ... In general, a standing wave will be established when the length 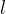 of the rope is:
of the rope is:
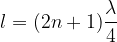
or, if we express in terms of the wavelength:

where 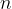 is zero or an odd natural number
is zero or an odd natural number 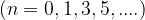
The wavelength of a standing wave in a plate that is clamped on one side and free on the other is calculated by the equation:
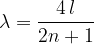
where 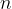 is the harmony (a multiple of the fundamental frequency), and
is the harmony (a multiple of the fundamental frequency), and 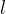 is the length of the rope.
is the length of the rope.
Let's calculate the oscillation frequency:
If 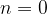 , we get the fundamental oscillation frequency (fundamental tone if it is a musical instrument), if
, we get the fundamental oscillation frequency (fundamental tone if it is a musical instrument), if  etc., we get higher harmonic components.
etc., we get higher harmonic components.
Let's take an elastic tile (e.g. made of wood or metal) and, without rigidly attaching it to a base, strike it with a hammer.
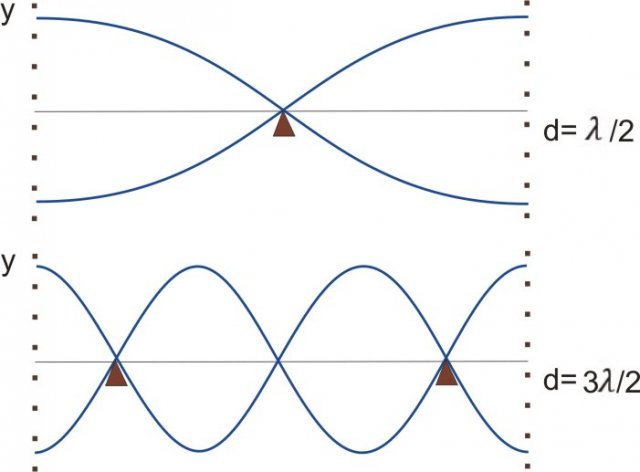
Figure 7: Free elastic plate on both sides - a) the fundamental oscillation frequency is shown b) the first harmonic frequency is shown. The triangle shows the place where the tile can be clamped - wave node
Because the plate is not clamped at the ends, it has a maximum oscillation amplitude at these points. In between is one, two, or more nodes where the tile is at rest - depending on the harmonic frequency with which the tile swings.
At the place where the small triangle is, the plate can be clamped to a base (example xylophone in Figure 1 - last instrument on the right).
From Figure 7, we see that for the fundamental oscillation, the length 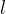 the rope will be equal to half of the wavelength:
the rope will be equal to half of the wavelength:
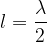
For the first harmonic frequency, the length of the rope will be:
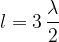
etc ... In general, a standing wave will be established when the length 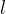 of the rope is:
of the rope is:
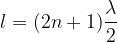
or, if we express in terms of the wavelength:

where 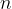 is zero or an odd positive integers
is zero or an odd positive integers 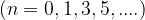
The wavelength of a standing wave in a plate that is free at both ends is calculated by the equation:
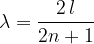
where 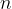 is the harmony (a multiple of the fundamental frequency), and
is the harmony (a multiple of the fundamental frequency), and 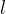 is the length of the rope.
is the length of the rope.
Let's calculate the oscillation frequency:
If 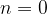 , we get the fundamental oscillation frequency (fundamental tone if it is a musical instrument), if
, we get the fundamental oscillation frequency (fundamental tone if it is a musical instrument), if  etc., we get higher harmonic components.
etc., we get higher harmonic components.