Personal collections


A pyramid is a geometric body whose surface consists of several flat surfaces. All the flat faces converge at a point above the base of the pyramid at a point called apex. The area below the top is called the base area.
We divide the pyramids into two large groups:
upright - the top lies just above the center of the base plane,
oblique - the top is offset from the center of the base area.
This is a somewhat loose description of upright and oblique pyramids. The properties of vertical pyramids will be discussed in more detail below.
As we have seen, there are several types of pyramids, and we can ascribe some common features to all of them. The properties of the pyramids will be looked at in detail below.
A pyramid is an geometric body bounded by:
base,
lateral surface sides.
The base surface of a pyramid is an n-angle.
The lateral of a pyramid consists of n triangles.
The pyramid is characterized by the following elements:
Base edges of a pyramid are the sides of the base plane (n-angle).
Side edges are all other edges of the pyramid. These are the lines that connect the vertices of the base plane to the top of the pyramid. The side edges therefore meet at the top of the pyramid.
The side faces of the pyramid are the triangles that make up the lateral surface of the pyramid.
The height of the pyramid is a line perpendicular to the base plane. Its length is equal to the distance between the base plane and the top of the pyramid.
Side heights are the heights of the lateral faces of the pyramid.
In the introduction, we saw that we distinguish between upright and oblique pyramids. Oblique pyramids are too demanding for the framework of primary school, so in the following we will focus only on vertical pyramids.
In the following, we consider only the upright pyramids.
A pyramid is upright if all the side edges are the same length. This, in turn, means that all the triangles that make up the mantle of the pyramid are isosceles. However, the triangles in the coat are not necessarily consistent. As we shall see below, the conformity of the side faces applies only to regular and uniform pyramids.
The following special features apply to the vertical pyramid:
side edges are consistent,
sides are isosceles triangles.
These features make it easier for us to calculate the area and volume of the pyramid, which we will learn about below.
The surface of a pyramid is its surface, which consists of several boundary surfaces. We calculate it by summing the areas of all its boundary surfaces. The boundary surfaces of the prism are:
polygon and
The entire surface of the pyramid is arranged in several planes. To make the surface easier to imagine, the boundary surfaces are spread out on one plane.
If we extend the boundary surfaces of the pyramid to the plane, we obtain the grid of the pyramid. The entire grid represents a composite geometric figure.
The boundary surfaces of a body spread out on a plane are called the grid of a geometric body.
The calculation of the area of the pyramid can be imagined as the calculation of the area of the composite geometric figure. In doing so:
first we calculate the areas of individual parts,
then add these areas.
The base of the pyramid is n-angle. Therefore, there is no single formula for calculating its area. However, we can write:
Let's denote the area of the base surface of the pyramid by 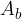 .
.
We calculate it in the same way as the area of an n-gon.
As we have already said, the lateral surface of an upright pyramid consists of isosceles triangles.
The area of the lateral surface of the pyramid is denoted by LSA.
The total area of the lateral surface of a pyramid is the sum of the areas of all the isosceles triangles that make it up.
The total surface area of the pyramid is calculated by summing the areas:
base area,
Lateral surface area.
The general equation for the total surface area TSA of the pyramid is:
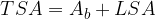
where 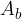 is the area of the base , and LSA is the area of the latera surface of the pyramid.
is the area of the base , and LSA is the area of the latera surface of the pyramid.
The volume of a pyramid is the size of the space that the pyramid takes up.
The general equation for calculating the volume V of a pyramid is:
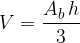
where 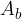 is the area of the base, and h is the height of the pyramid.
is the area of the base, and h is the height of the pyramid.
We know several types of pyramids, which are distinguished by their properties. The properties of pyramids are the basis for their naming. Let's see what properties distinguish them.
The pyramid is named after the n-angle, which represents the base surface.
In general we can write:
A pyramid whose base is n-angle is called an n-sided pyramid.
Let’s focus on the edges of the pyramid. Specific examples are pyramids that have the following:
regular base,
all the edges in the pyramid.
Let’s look at both groups of pyramids in more detail.
A pyramid that has consistent base edges is called a regular base pyramid.
The base edges represent the sides of the base area. A polygon with the same length of sides is correct, so we write similarly for the pyramid.
A pyramid is correct if it has a regular n-gon for the base surface.
If a pyramid has all the edges (both base and lateral) of the same length, it is called a regular pyramid.
A pyramid is equilateral if all the edges have the same length.
For the equilateral pyramid we can also write the following:
A pyramid that is equilateral is also regular at the same time.
For special cases of pyramids, simplified forms for calculating area and volume apply. We derive them from the basic formulas taking into account the properties of each pyramid.
We will look at some examples in more detail:
three-sided,
four-sided
vertical pyramids.
Let’s look at the three-sided pyramids first.
A regular three-sided pyramid has an equilateral triangle as its base:
Area
To facilitate the calculation of the area, we draw a grid of the pyramid:
The plane of the base plane of a right three-sided pyramid is equal to the plane of an equilateral triangle:
The equation for the area of the base plane of a regular three-sided pyramid is:
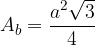
wherea is the length of the base edge of the pyramid.
The lateral surface of the pyramid consists of three consistent isosceles triangles. We denote the area of the triangle in the lateral surface by 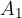 and derive the equation for calculating the lateral surface area of a regular three-sided pyramid. We start from the equation:
and derive the equation for calculating the lateral surface area of a regular three-sided pyramid. We start from the equation:
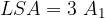
We derive it in terms of the height 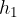 :
:
We have obtained the equation for the lateral surface area of the regular three-sided pyramid.
The equation for the lateral surface area of a regular three-sided upright pyramid is:
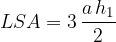
wherea is the length of the base edge and 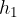 is the side height of the pyramid.
is the side height of the pyramid.
We also derive the equation for the total surface area of the regular three-sided pyramid with the general equation for the area of the pyramid:

We derive it:
We obtained the equation for the area of a regular three-sided pyramid.
The equation for the area of a regular three-sided pyramid is:
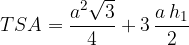
wherea is the length of the base edge and 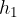 is the side height of the pyramid.
is the side height of the pyramid.
To calculate the slant height 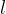 we can use the side height
we can use the side height 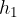 .
.
The side face of the pyramid is an isosceles triangle. If we halve it perpendicular to the base, we get two right triangles:
For both the left and right right triangles we can write Pythagoras theorem:
When calculating the slant height of a pyramid, we use the Pythagorean theorem on a right triangle:
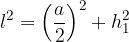
where l is the length of the side edge, a is the length of the base edge, and 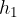 is the side height of the pyramid.
is the side height of the pyramid.
The rule applies generally to all regular upright pyramids.
Volume
We derive the equation for the volume of a regular three-sided pyramid with the general equation for the volume of the pyramid:
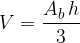
Write it down:
We have obtained the equation for the volume of an equilateral triangular base pyramid.
The equation for calculating the volume of a regular three-sided pyramid is:

where a is the length of the base edge, and v is the height of the pyramid.
The four-sided vertical pyramid has a rectangle for the base surface:
Area
To facilitate the calculation of the area, we draw a grid of the pyramid:
The area of the base surface of a four-sided pyramid is equal to the area of the rectangle:
The equation for the area of the base plane of a four-sided pyramid is:
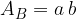
where a and b the length and width of the base plane of the pyramid.
Let's write another equation for calculating the lateral surface area. The side faces are isosceles triangles to which:
all sides are the same length,
two opposing bases are the same.
The triangles that make up the lateral surface area of the pyramid are therefore in pairs. We denote the area of the first pair by  and the second by
and the second by  .
.
To get the area of the lateral surface, we will start from the equation:

We derive the equation for the area of the lateral:
We obtained the equation for the area of the mantle of the four-sided pyramid.
The equation for the area of the mantle of a four-sided pyramid is:
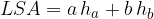
where a and b are the length and width of the base plane, and 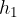 and
and 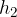 are the side heights of the pyramid.
are the side heights of the pyramid.
Each side face of the pyramid is an isosceles triangle. These isosceles triangles can be of different sizes. The pyramid, which has a rectangle as its base, has in the lateral:
two isosceles triangles with base a and
two isosceles triangles with base b
If we bisect an isosceles triangle with the base a perpendicular to the base, two right triangles are formed, for which we can write The Pythagorean Theorem, with which we calculate the side edge of the pyramid:
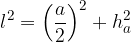
In the same way as above, halve the isosceles triangle with the base b. In this case, too, two right triangles are formed, for which we can write The Pythagorean Theorem:


Left - right triangle on the side face of a right three-sided pyramid with base a,
right - right triangles on the side face of a right three-sided pyramid with base b
Write down the rule for using the Pythagorean theorem in calculating the side edge of a pyramid:
When calculating the side edges  we use the Pythagorean theorem on a right triangle:
we use the Pythagorean theorem on a right triangle:
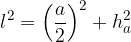

where a and b are the lengths of the base edges, and 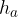 and
and 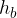 are the side heights of the pyramid.
are the side heights of the pyramid.
We also derive the equation for the total surface area of an upright four-sided pyramid with the general equation for the area of the pyramid:
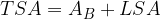
Let's derive:
We obtained the equation for the total surface area of an upright four-sided pyramid.
The equation for the total surface area 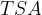 of an upright four-sided pyramid reads:
of an upright four-sided pyramid reads:
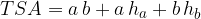
where a and b are the length and width of the base plane, and 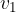 and
and 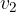 are the side heights of the pyramid.
are the side heights of the pyramid.
Volume
We also derive the equation for the volume of an upright four-sided pyramid with the general equation for the volume of the pyramid:
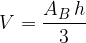
Let's derive:
We obtained the equation for the volume of an upright four-sided pyramid.
The equation for calculating the volume 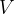 of an upright four-sided pyramid is:
of an upright four-sided pyramid is:
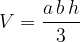
where a and b the length and width of the base plane, and h the height of the pyramid.
Forms for calculating side heights and side edge
If we cut a four-sided pyramid with the plane on which the height of the pyramid lies and two of the side heights, we get an isosceles triangle. Two cross-sections are possible:
cross section parallel to the side a
cross section parallel to the side b
In both cases, we divide an isosceles triangle perpendicular to the base and obtain two right triangles in which the Pythagorean theorem holds:
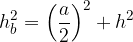
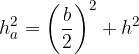
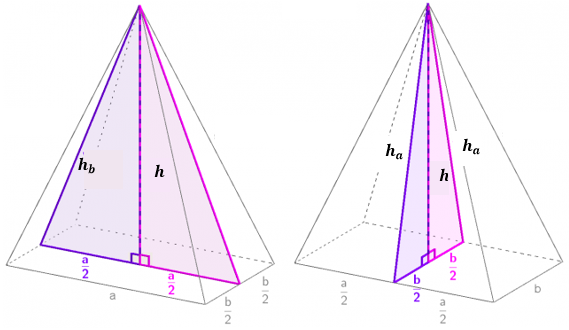
Left: section of the four-sided pyramid parallel to the base edge a, right: section of the four-sided pyramid parallel to the base edge b
Let us write Pythagoras' theorem again:
Height, side heights, and base edges are connected in a four-sided pyramid through Pythagorean theorems:
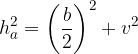

where 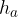 and
and 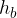 are the side heights, a and b the length and width of the base plane, and h the height of the pyramid.
are the side heights, a and b the length and width of the base plane, and h the height of the pyramid.
The four-sided pyramid can also be cut with the plane on which the top of the diagonal of the base plane 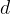 lies. On this plane lies the height of the pyramid and two of the side edges. Here, too, we obtain an isosceles triangle:
lies. On this plane lies the height of the pyramid and two of the side edges. Here, too, we obtain an isosceles triangle:
We halve the isosceles triangle perpendicular to the base. We obtain two right triangles in which Pythagoras' theorem holds:

Write it down:
The height, side edges, and diagonals of the base plane are connected in a four-sided pyramid by the Pythagorean theorem:

where l is the slant height, d is the diagonal of the base plane, h is the height of the pyramid.
A regular four-sided vertical pyramid has a square as its base:
Area
To facilitate the calculation of the area, we draw a grid of the pyramid:
The area of the base area of a regular four-sided pyramid is equal to the area of the square.
The equation for the area of the base of a regular four-sided upright pyramid is:
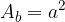
where a is the length of the base edge of the pyramid.
The lateral surface of the pyramid consists of four consistent isosceles triangles. We denote the areas of the triangles in the lateral surface by 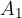 and derive the equation for the area of the lateral surface of a regular four-sided pyramid. The derivation is based on the equation:
and derive the equation for the area of the lateral surface of a regular four-sided pyramid. The derivation is based on the equation:
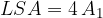
Let's derive the equation for the lateral surface area:
We obtained the equation for the area of the lateral surface of a regular four-sided pyramid.
The equation for the area of the lateral surface 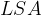 of a regular upright four-sided pyramid is:
of a regular upright four-sided pyramid is:
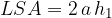
where a is the length of the base edge and 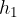 is the side height of the pyramid.
is the side height of the pyramid.
The side face of the pyramid is an isosceles triangle. If we halve it perpendicular to the base, we get two right triangles:
For both the left and right right triangles we can write The Pythagorean Theorem:
When calculating the slant height 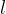 of the pyramid, we use the Pythagorean theorem on a right triangle:
of the pyramid, we use the Pythagorean theorem on a right triangle:
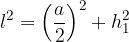
where a is the length of the base edge and 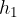 is the slant height of the pyramid.
is the slant height of the pyramid.
We also derive the equation for the total surface area of a regular four-sided pyramid with the general equation for the area of the pyramid:

Let's derive it:
We obtained the equation for the total surface area of a regular four-sided pyramid.
The equation for the total surface area 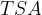 of a regular four-sided upright pyramid is:
of a regular four-sided upright pyramid is:
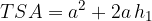
where a is the length of one side of the base and 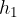 is the slant height of the pyramid.
is the slant height of the pyramid.
Volume
We also derive the equation for the volume of a regular vertical four-sided pyramid with the general equation for the volume of the pyramid:
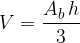
Let's derive it:
We obtained the equation for the volume of a regular upright four-sided pyramid.
The equation for calculating the volume 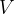 of a regular three-sided upright pyramid is:
of a regular three-sided upright pyramid is:
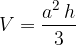
where a is the length of one side of the base, and h is the height of the pyramid.
Forms for side height and side edge
The correct four-sided pyramid can be cut through the top:
at opposite lateral heights 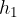 ,
,
diagonally 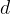 base plane.
base plane.
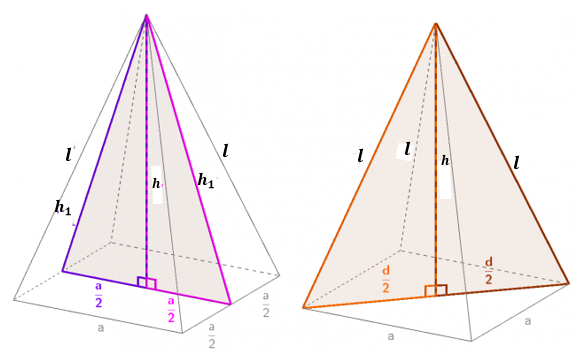
Left: section of a regular four-sided pyramid parallel to the base edge a, right: section of a regular four-sided pyramid parallel to the diagonal of the base plane d
In both sections we get an isosceles triangle. This isosceles triangle is halved into two right triangles, on which we can use the Pythagorean theorem. This gives us two forms to help us calculate in the tasks:
The height, side heights, and base edges are connected in a regular four-sided pyramid by the Pythagorean theorem:
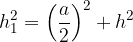
where 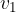 is the side height, a the base edge, and v the height of the pyramid.
is the side height, a the base edge, and v the height of the pyramid.
The slant height, side edges, and diagonals of the base plane are connected in a four-sided pyramid by the Pythagorean theorem:

where l is the slant height, d is the diagonal of the base plane, h is the height of the pyramid.