A sphere is a geometric body whose surface consists of a single, self-contained curved surface. The area bounding the sphere is called a surface area, a ball, or a shell.
A sphere is a round geometric body with every point on its surface equidistant from its centre.
The sphere is characterized by the following elements:
ball or shell is a curved surface that bounds a sphere.
A shell is a set of points that are equal to the radius and at equal distances from the centre of the sphere.
Main sphere circle is the cross section of a sphere with a plane passing through the center of the sphere.
The main sphere divides the sphere into two hemispheres.
Specific elements of the sphere
The surface area of the sphere is the outer area bounding the sphere.
The equation for the area of a sphere P reads:
where R is the radius of the sphere.
The volume of a sphere is the size of space that the sphere occupies.
The equation for calculating the volume of a sphere V reads:
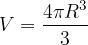
where R is the radius of the sphere.
Let's cut an orange through its centre. This creates two hemispheres.
Half-cut orange
Each of the hemispheres has one curved and one flat round surface. A flat round surface is the main spherical circle.
Cut the sphere with a plane that does not pass through the center, but is distant from it by a distance v. The intersection of a sphere and a plane is a circle that is smaller in size than the main spherical circle. We call it a spherical circle.
The plane divides the sphere into two parts. The smaller part is called the spherical section. The surface of a spherical section consists of one curved and one flat round surface. A curved surface is called a spherical cap, and a flat one is called a spherical circle:
Spherical section
Spherical circle is the cross section of a sphere with a plane at a distance h from the centre of the sphere.
A spherical section is a smaller part of a sphere cut by a plane at a distance h from the center of the sphere.
Spherical cap is a smaller part of a spherical sphere cut by a plane at a distance h from the center of the sphere.
In a sphere with a section at a distance h from the centre we see a right triangle for which Pythagoras theorem holds:
Pythagoras theorem in a sphere
The distance of the spherical section from the centre of the sphere h, the radius of the sphere R and the radius of the spherical section r are related to each other by the following Pythagorean theorem:
