Surface tension is observed at the boundary between a liquid and a gas. Surface tension is the phenomenon that causes the surface of a liquid to behave like a stretched membrane on which a light object can be placed - and the object remains on the surface (see Figure 1). The upthrust force is not involved here since the density of the body can be greater than the density of the liquid.
Surface tension is observed when a liquid is at rest at lower temperatures. The thermal motion of molecules at higher temperatures weakens the phenomenon of surface tension.
We will see that the cause of surface tension is the weak attractive intermolecular forces in liquids. They are called Van der Waals forces. These are distributed differently on the surface than in depth. They act tangentially to the surface by stretching it. If the liquid bulges due to the action of gravity (see Figures 1 and 2), the force of surface tension acts tangentially to the curvature of the surface and tends to flatten it.
Intermolecular forces act between the molecules of the liquid. We already learned about the forces between molecules in the chapter, Deformation of solids. If the distance between the molecules is:
greater than the radius of the molecule, the forces are attractive,
smaller than the radius of the molecule, the forces are repulsive. Since the liquid is almost incompressible, the repulsive force increases steeply as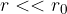 
.
Let's observe a water molecule deep enough below the surface. Let us assume that initially, the distance of the neighboring molecule from the observed one is much greater than the radius of the molecule:
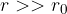
Let us assume that at this distance, the potential energy of the molecule is zero. Let's recall that we can arbitrarily determine where the potential energy will be zero. Due to the attractive force 
, the molecule approaches the observed molecule to a distance of 
. Its potential energy is falling, becoming negative. At distance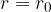 
, it reaches a maximum negative value 
(see Figure 3).
Figure 3: Potential energy of a liquid molecule
The attractive forces between molecules in liquids have a short range. Its effects extend only to a distance of several times the radius of the molecule. Assume that only N neighboring molecules contribute to the potential energy. The total potential energy is:
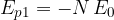
A molecule located on the surface is acted upon by half as many neighboring molecules, so its potential energy is halved (see Figure 4):
Figure 4: The set of molecules that contribute to the potential energy of the observed molecule
The difference between the potential energy of a molecule on the surface and below the surface is:
The potential energy of a molecule on the surface is greater than the potential energy of a molecule below the surface!
Let's go back to the phenomenon when the water level exceeds the edge of the glass. We can see that the surface area is larger than the cross-section of the glass - the surface area is rounded. Since the surface area is larger than the cross-section of the glass, this means that we had to bring additional molecules to the surface.
If we simplify the calculation, we can say that the surface area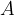 
of one molecule is 
and the number of molecules that we need to bring to the surface area to increase it by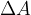 
, is given as:
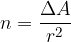
We bring n additional molecules to the surface, so the total potential energy increases by:
To increase the surface area, we need to move the internal molecules to the surface. We need energy for that. The change in potential energy is proportional to the change in surface area. The proportionality constant is the surface tension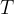 
:
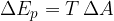
Let's take a frame with a movable bar of length 
. We dip the frame into, for example, soapy water so that a membrane is formed over the entire surface. If no force acts on the bar, the membrane wants to move it in the direction of decreasing the total area in the frame. Let's act on the bar with a force by moving it by 
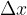(see Figure 5). The total surface area of the soap bubble increases by 
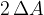. The factor 2 was taken because the membrane actually has twice the boundary surface compared to air.
Figure 5: Soap membrane, tensioned on a frame.
If we want to increase the total surface by 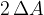, we must do work 
, which is equal to the change in the potential energy of the surface of the liquid:
The table below shows the surface tension of some selected liquids.
Surface tension 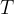tells us how much work we have to do to increase the surface area of a liquid by :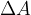
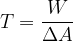
The unit is:
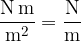
The surface tension force is directed tangentially to the surface and acts in the direction of decreasing the surface area. We calculate it using the equation:
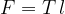
where is the length of the boundary edge of the liquid. If the membrane of liquid borders the air on both sides, we have to take double the length :
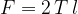
In the previous chapter, we limited ourselves to the phenomenon of surface tension at the contact between liquid and gas (air). There are also other boundary surfaces on which surface tension occurs. In addition to liquid and gas, these are also the boundary between:
solid and liquid, and
solid and gas.
All three surface tensions affect the shape of the surface of the liquid in contact with the solid and the gas.
The kind of liquid droplet formed depends on the surface tension on all surfaces adjacent to the droplet. To explain this phenomenon, we extend the concept of surface tension to the surface tension between two substances, e.g. liquid and air, liquid and solid, solid and air, or between two liquids.
Why does surface tension occur when different substances of the same or different states (solids, liquids, gases) come into contact?
A qualitative explanation of why surface tension occurs between liquid and gas was initially given based on the change in potential energy caused by weak Van der Waals forces. They act attractively, and when the molecules come together in clusters, they lose potential energy. We have seen that the drop in potential energy depends on whether we observe the molecules inside the substance or at the boundary with the gas (e.g. air).
Similarly, weak forces also act on the contact of any two substances of the same or different states. The potential energy is different inside the substance than on its boundary surface. And it depends on the two substances that come into contact.
Let's go back to the drop. The liquid takes the shape that has the least total energy. This consists of surface energy and potential energy due to weight. Neglecting potential energy due to weight, the most favourable shape is a sphere. It has the smallest surface area for a given volume. If the droplet is large, it flattens a bit, its centre of gravity (potential energy) decreases. The total energy is still the smallest. We say that the liquid is in a stable equilibrium state.
At the contact line gas - liquid - solid (substrate), there are three surface tensions (see Figure 9):
Surface tension between liquid and gas: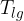 
Surface tension between liquid and solid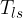 
Surface tension between solid and gas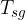 
Figure 9: Surface tension forces at the edge of 3-boundary surfaces
The horizontal components of the forces on the edge of the droplet must cancel for the droplet to rest. From this condition, we express the angle that the drop makes with the base.
The table below shows the angles of contact for some selected solids and liquids:
The angle of contact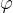 
indicates the wetting phenomenon between the solid and liquid in contact (see Figure 10). If the angle of contact is less than 
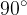, the solid is wetted by the liquid. If greater than 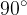, the solid does not get wet. The limit angle between the wetted or non-wetted solid is .
Figure 10: Angle of contact (wetting angle)
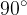The angle of contact is the angle between the surface of the liquid and the solid. If the angle of contact is less than 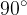, the solid is wetted. If it is greater than 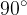, the solid does not get wet.
In the introduction, we mentioned that liquid can travel, e.g. water through thin tubes called capillaries, upwards, without the need for additional force or pressure. Capillarity in plants allows water to reach all parts of the plant from the roots. The phenomenon is called capillary pressure and is the result of surface tension.
Capillary pressure depends on the angle of contact (wetting angle) between the capillary wall and the liquid. If the wetting angle is less than 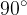, the liquid rises through the tube above the surface, if it is greater, the level in the capillary is lower.
How do we calculate the rise of liquid in a capillary tube? Let's see Figure 11 below:
Figure 11: Water rises in a capillary tube
The vertical component of the surface tension force , on the other hand, is equal to the force of the weight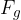 
of the fluid in the capillary:
How much liquid rises or falls through a capillary depends on the surface tension 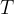of the liquid, the angle of contact (wetting angle) 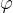between the liquid and the substance from which the capillary is made, the density 
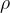of the liquid and the radius 
of the capillary:
