Given a right-angled triangle as shown below:
The side b is adjacent to the angle α and the side a is opposite the angle α.
The tangent of the angle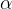 
is defined as the ratio between the opposite side (a) and the adjacent side (b):
The cotangent of the angle 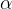is defined as the ratio between the adjacent side (b) and the opposite side (a):
A unit circle
We draw the tangent and cotangent functions on a unit circle:
Tangent and cotangent functions on a unit circle
The values of tangent and cotangent are a bit harder to read from the unit circle, so we will use the sine and cosine values we already know to draw (we will just expand the table and calculate values from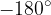 
to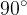 
), it will be much easier to draw tangent and cotangent using these values.
To calculate the tangent and cotangent we use the formula:
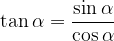
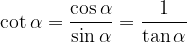
The value of the angle α is expressed in radians. This means that the value π is equal to 3.14159 ... and not 180°.
Let us draw the tangent function. We enter the values of the angle α on the x axis, and the value of the tangent on the y axis:
When drawing the tangent function as α we refer to the x axis. Therefore, when considering the graph, instead of the notation α, we use the notation x.
We read the values from the table and compare them with the graph - the values must be the same:
We start by reading the value in the table with angle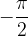 
and get the value 
,
the next value α we are considering is equal to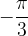 
, we read the value 
,
we continue with angle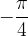 
, we read the value of the tangent as 
,
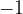at angle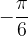 
we read the value of 
,
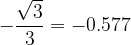at angle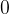 
we read the value of the tangent as ,
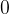when the angle α is equal to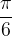 
, we read from the table the value of the tangent function is 
,
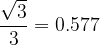when the angle α on the unit circle is increased to 
, the tangent reaches the value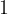 
,
when we increase the angle α to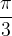 
, we read the value of the tangent 
,
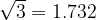when α is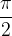 
, we read the value of the tangent 
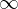, from here on the values begin to repeat, we can conclude that the tangent is repeated on every 
.
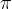We made one round around the table; if we make a new round, all the steps will be repeated. Obviously, the function will be repeated at spaces .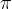
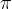is therefore the period of the function.
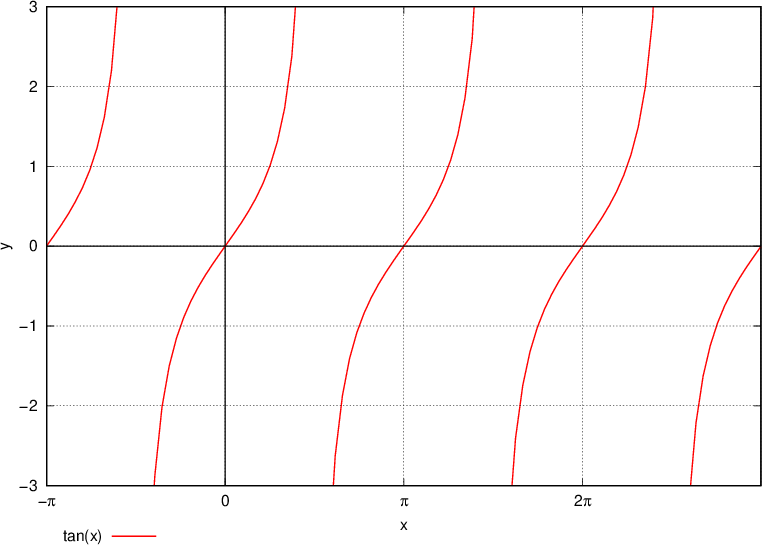
The tangent function is periodic with period 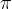. Periodicity / repetition can be easily observed on the graph.
The procedure is repeated for the cotangent - we read the values from the table and compare them with the graph - the values must be the same.
We start by reading the value in the table with the angle 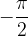and get the value .
The next value α we are considering is equal to 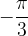, we read the value .
We continue at an angle 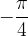, we read the value of the cotangent as .
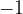At the angle 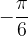we read the value 
.
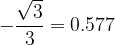At the angle 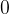we read the value of the cotangent as .
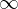When the angle α is equal to 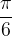, we read in the table the value of the cotangent function equal to .
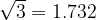When the angle α on the unit circle is increased to , the cotangent reaches the value .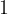
When we increase the angle α to 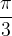, we read the cotangent value .
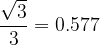We increase the angle α to 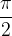, we read the value of the cotangent as 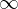, from here the values start repeating, we can conclude that the cotangent repeats every .
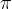We made one round around the table; if we make a new round, all the steps will be repeated. Obviously, the function will be repeated at spaces .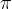
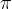is therefore the period of the function.
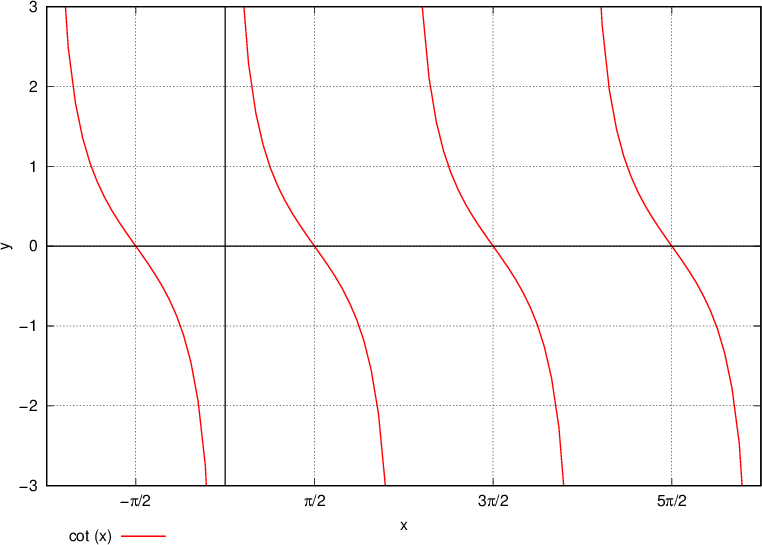
The cotangent function is periodic with the period 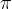. Periodicity / repetition can be easily observed on the graph.
The properties of both functions are most easily read from the graph. In the following, we will describe the properties we learned about through the graph in a mathematical way.
The domain 
includes all those x that can be plotted on the graph and for these x values, the function exists.
Tangent and cotangent are defined as fractions (see introduction to the material). We know that a fraction cannot exist (it is not defined) if the denominator is equal to 0, so we will exclude from the domain all those values of functions for which we get the value of 0 at the denominator. These values are called vertical asymptotes.
The range of values includes all those y-values that appear on the graph.
The tangent function is defined as
The tangent has a vertical asymptote exactly when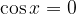 
(cosine zeros), and this is the case for every
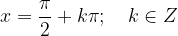
The domain of the tangent function is the entire real axis x except 
, or written as:
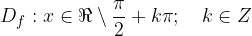
From the graph of the tangent function and in the table, we can see that the range of values is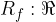 
.
The range of values of the tangent function is:
The cotangent function is defined as
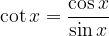
The cotangent has an asymptote when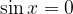 
(sine zero), and this is the case for every
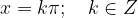
The domain of the cotangent function is the entire real axis x except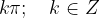 
.
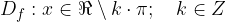
The range of values includes all those y that appear on the graph. From the cotangent graph of the function and in the table, we can observe that the range of values is .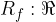
The range of values of the cotangent function:
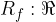
The zeros of a function are those points where the function intersects the x-axis.
Tangent zeros are obtained for each multiple of 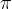, or, the tangent function has a value of zero for angles:
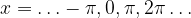
or, in other words:
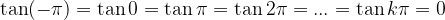
The tangent zeros are obtained with the attachment:
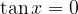
The solution of the attachment is:
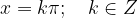
The cotangent zeros are obtained for each multiple of 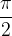(the cosine zeros).
or, in other words:
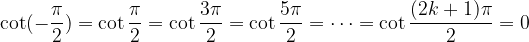
The zeros of the cotangent are obtained by solving:
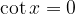
The solution of which are:
The discontinuous points of the tangent function are obtained for each multiple of 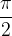(for cosine zeros), or, the tangent does not exist at these values (not defined).
or, in other words:
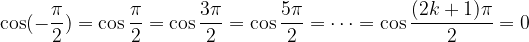
The discontinuous points are obtained by solving:
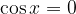
The solution of which are:
The discontinuous points of the cotangent functions are obtained for each multiple of 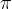(sine zeros):
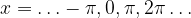
or, in other words:
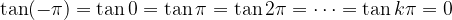
The discontinuous points of the cotangent function are obtained by solving:
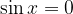
The solutions of which are:
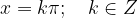
A function is odd if it is symmetric with respect to the coordinate origin, or when:
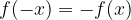
A function is an even if it is symmetric with respect to the y-axis:
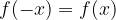
The tangent function is true when:
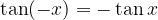
which can also be deduced from the graph (the function is symmetric with respect to the coordinate origin). Apparently, the tangent function is an odd function.
The following applies to the cotangent function:
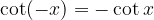
which can also be deduced from the graph (the function is symmetric with respect to the coordinate origin). Apparently, the cotangent function is an odd function.
The rising tangent is very easy to deduce from the graph. The function grows throughout its domain .
The falling cotangent is also easy to understand. Cotangent falls throughout its domain .
The tangent and cotangent functions are periodic over 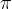. Periodicity / repetition can be easily observed from the graph.
The tangent function is repeated every .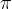
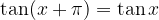
The cotangent function is repeated every .
The tangent and cotangent functions are discontinuous. The graph shows this where they "break" at the vertical asymptote.
