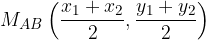Two points 
and 
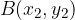are given in the rectangular coordinate system. We want to calculate the distance between them or the length of the distance 
.
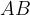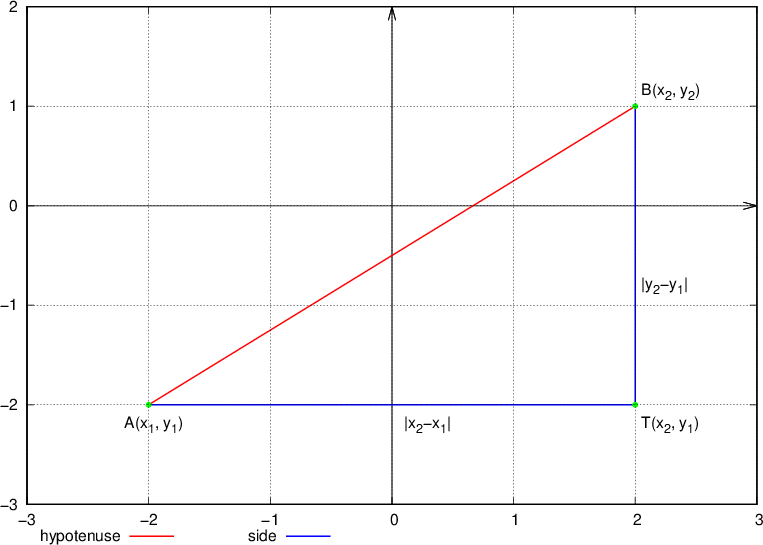
From the sketch, we notice that we are dealing with a right triangle, which means that we can use Pythagoras' theorem:
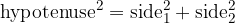
The distance between two points is always a non-negative number, so we use an absolute value for the length of the side of a right triangle. Hence, the two sides are written as:
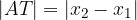
Let’s use Pythagoras' theorem to calculate the hypotenuse or the length of 
:
Equation for the distance between two points:
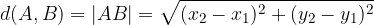
The mark for distance d is the first letter of the Latin word distancia, which means distance.
The distance between any points is always a non-negative number:
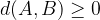
The distance between two points is equal to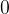 
exactly when the points coincide:
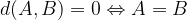
The distance from point A to point B is equal to the distance from point B to point A:
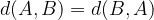
The distance from A to C is less than or equal to the sum of the distances from A to B and from B to C:
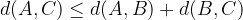
The arithmetic mean of the two values x and y is equal to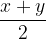 
.
The midpoint of the line with the ends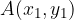 
and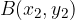 
is the point::
