Personal collections


Each pair of natural numbers has at least one common divisor, that is, the number 1.
Common divisors of two numbers 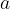 and
and 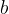 are the number 1, common prime factors, and all possible products of common prime factors if they exist.
are the number 1, common prime factors, and all possible products of common prime factors if they exist.
The highest common factor of the two numbers 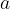 and
and 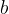 , is the highest/greatest divisors that divide both numbers.
, is the highest/greatest divisors that divide both numbers.
Let us denote it by

The highest common factor is obtained as the product of all common prime factors, including multiples.
We can also look for common divisors of several numbers. Then the greatest common divisor is the product of all common prime factors of all numbers.
Every two natural numbers have infinitely common multiples.
To find the greatest common divisor we can also use a computational procedure called the Euclidean algorithm. The greatest common divisor is the last remainder in an algorithm other than 0. In the Euclidean algorithm procedure, we use the basic division theorem 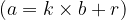 at each step.
at each step.
Let's look at some examples.