This method is quite similar to the tangent method of finding zeros, except that it assumes that the secant on the polynomial behaves similarly to the polynomial and therefore its zero is similar to the zero of the polynomial. In this method, we have to select two points on the polynomial, which are the initial approximations of our zero (preferably, the sign of the given polynomial should differ at these points).
Using the sketch above, let’s look at how to find the zero of a secant on a given polynomial. First, we write down the gradient of the secant. This can be written in two ways:
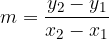
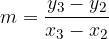
By equating the two gradients, we obtain the iterative formula for the secant method:
So we got the iterative formula for the secant method.
The iterative formula for the secant method is:
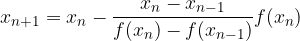
where:
the inverse of the gradient of the secant and
the pre-selected point.
Let’s look at the method using a practical example.
